- Связное множество
-
Курсив обозначает ссылку на этот словарь
# А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Э Ю Я
Б
- База топологии — набор открытых множеств, такой, что любое открытое множество является объединением множеств из базы.
В
- Внутренность — совокупность всех внутренних точек множества.
- Внутренняя точка множества — точка, у которой есть окрестность, содержащаяся в данном множестве.
- Выколотая окрестность точки p — это окрестность p с вырезанной p.
- Всюду плотное множество — множество, замыкание которого совпадает со всем пространством.
Г
- Гомеоморфизм — биекция f, такая, что f и f − 1 непрерывны.
- Гомеоморфные пространства — пространства, между которыми существует гомеоморфизм.
- Гомотопия непрерывного отображения
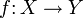 есть непрерывное отображение
есть непрерывное отображение ![F\colon[0,1]\times X\to Y](/pictures/wiki/files/49/14c0dffc35f67ba4fa92aefd60fcdf4f.png) , такое, что F(0,x) = f(x) для любого
, такое, что F(0,x) = f(x) для любого 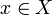 . Часто используется обозначение ft(x) = F(t,x), в частности f0 = f
. Часто используется обозначение ft(x) = F(t,x), в частности f0 = f - Гомотопные отображения. Отображения
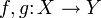 называются гомотопными или
называются гомотопными или 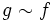 если существует гомотопия ft такая, что f0 = f и f1 = g.
если существует гомотопия ft такая, что f0 = f и f1 = g. - Гомотопическая эквивалентность топологических пространств X и Y есть пара непрерывных отображений
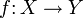 и
и 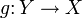 такая, что
такая, что 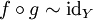 и
и 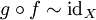 , здесь
, здесь 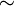 обозначает гомотопическую эквивалентность отображений. В этом случае говорят, что X и Y гомотопически эквивалентны, или X с Y имеют один гомотопический тип.
обозначает гомотопическую эквивалентность отображений. В этом случае говорят, что X и Y гомотопически эквивалентны, или X с Y имеют один гомотопический тип. - Гомотопический инвариант — это характеристика пространства, которая сохраняется при гомотопической эквивалентности топологических пространств. То есть, если два пространства гомотопически эквиваленты, то они имеют ту же характеристику. Например: связанность, фундаментальная группа, эйлерова характеристика.
- Гомотопический тип — см. гомотопическая эквивалентность.
- Граница. Смотри относительная граница или граница многообразия.
- Граница многообразия. Смотри многообразие.
Д
- Деформационный ретракт
- Дискретная топология. Топология, в которой любое множество открыто.
- Дискретное множество. Множество, каждая точка которого является изолированной.
- Дикий узел
З
- Замкнутое множество — дополнение к открытому.
- Замкнутое отображение — такое отображение, что образ любого замкнутого множества замкнут.
- Замыкание. Минимальное замкнутое множество, содержащее данное.
И
- Индуцированная топология — топология на подмножестве A топологического пространства, открытыми множествами в которой считаются пересечения открытых множеств объёмлющего пространства с A.
- Изолированная точка множества A топологического пространства X — такая точка
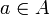 , что пересечение некоторой её окрестности с A состоит из единственной точки a.
, что пересечение некоторой её окрестности с A состоит из единственной точки a.
К
- Категория Бэра
- Компактное пространство
- Компонента связности точки есть максимальное связное множество, содержащее эту точку.
- Континуум — связное компактное хаусдорфово топологическое пространство.
- Конус над топологическим пространством X (называемым основанием конуса) — пространство CX, получающееся из произведения
![X\times[0,\;1]](/pictures/wiki/files/102/fab76c8fbbfaa0f572b4af49a579ff27.png) стягиванием подпространства
стягиванием подпространства 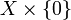 в одну точку, называемую вершиной конуса.
в одну точку, называемую вершиной конуса. - Край многообразия, см. многообразие
- Кривая есть непрерывное отображение связного подмножества вещественной прямой.
Л
- Линейно связное пространство. Пространство, в котором любую пару точек можно соединить кривой.
- Локально компактное пространство. Пространство, в котором любая точка имеет компактную окрестность.
- Локально связное пространство. Пространство, в котором любая точка имеет связную окрестность.
- Локально стягиваемое пространство. Пространство, в котором любая точка имеет стягиваемую окрестность.
- Локальный гомеоморфизм — отображение
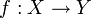 топологических пространств, такое, что для каждой точки
топологических пространств, такое, что для каждой точки 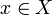 найдется окрестность Ux, которая посредством f отображается в Y гомеоморфно. Иногда в определение локальный гомеоморфизм автоматически включается требование f(X) = Y и, кроме того, отображение f предполагается открытым.
найдется окрестность Ux, которая посредством f отображается в Y гомеоморфно. Иногда в определение локальный гомеоморфизм автоматически включается требование f(X) = Y и, кроме того, отображение f предполагается открытым.
М
- Массивное множество ― подмножество S топологического пространства X, являющееся пересечением счётного числа открытых плотных в X подмножеств. Если каждое массивное множество плотно в X, то X является пространством Бэра.
- Метризуемое пространство. Пространство, гомеоморфное метрическому пространству.
- Многообразие
- Многосвязная область линейно связного пространства — область, фундаментальная группа которой не тривиальна.
- Множество Бореля есть множество из Борелевской сигма-алгебры
- Множество второй категории. Любое множество, которое не является множеством первой категории.
- Множество первой категории. Множество, которое можно представить как счётное объединение нигде не плотных множеств.
Н
- Накрытие
- Непрерывное отображение — такое отображение, при котором прообраз любого открытого множества открыт.
- Нигде не плотное множество — множество, замыкание которого не содержит открытых множеств.
О
- О́бласть — открытое связное подмножество топологического пространства.
- Односвя́зное простра́нство — связное пространство, любое отображение окружности в которое гомотопно постоянному отображению.
- Окрестность — открытая окрестность или множество, содержащее открытую окрестность.
- Откры́тая окре́стность точки или множества — открытое множество, содержащее точку или множество.
- Откры́тое мно́жество основное понятие общей топологии, смотри Топологическое пространство.
- Откры́тое отображе́ние — такое отображение, что образ любого открытого множества открыт.
- Относи́тельная грани́ца. Пересечение замыкания подмножества топологического пространства с замыканием его дополнения. Граница множества E обычно обозначается
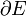 .
. - Относи́тельная топология — то же, что Индуцированная топология.
- Относи́тельно компа́ктное мно́жество — подмножество M топологического пространства T называется относительно компактным или предкомпа́ктным если его замыкание компактно.
П
- Паракомпактное пространство — топологическое пространство, из любого открытого покрытия которого можно выделить локально конечное подпокрытие (то есть такое, что для любой точки можно найти окрестность пересекающуюся с конечным числом элементов этого подпокрытия).
- Плотное множество
- Подпокрытие покрытия {Vα},
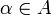 — это покрытие {Vβ}, где
— это покрытие {Vβ}, где 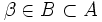 .
. - Подпространство — подмножество топологического пространства, снабжённое индуцированной топологией.
- Покрытие подмножества или пространства X — это представление его в виде объединения множеств {Vα},
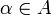 , точнее это набор множеств {Vα},
, точнее это набор множеств {Vα}, 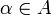 такой что
такой что 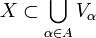 . Чаще всего рассматривают открытые покрытия, то есть предпологают что все {Vα} являются откытыми множествами.
. Чаще всего рассматривают открытые покрытия, то есть предпологают что все {Vα} являются откытыми множествами. - Предбаза — семейство Y открытых подмножеств топологпческого пространства X такое, что совокупность всех множеств, являющихся пересечением конечного числа элементов Y, образует базу X.
- Предельная точка подмножества A топологического пространства X — такая точка
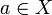 , что в любой её выколотой окрестности с A есть хотя бы одна точка из A.
, что в любой её выколотой окрестности с A есть хотя бы одна точка из A. - Производное множество — совокупность всех предельных точек.
Р
С
- Связное пространство. Пространство, которое невозможно разбить на два непустых непересекающихся (<=> dis, дизъюнктное) открытых множества.
- Сепарабельное пространство — топологическое пространство, в котором имеется счётное всюду плотное множество.
- Стягиваемое пространство — пространство, гомотопически эквивалентное точке.
T
- Топологический инвариант — характеристика пространства, которая сохраняется при гомеоморфизме. То есть если два пространства гомеоморфны то они имеют ту же характеристику. Например: компактность, связанность, фундаментальная группа, Эйлерова характеристика.
- Топологическое пространство
- Топология компактной сходимости. Топология, заданная на множестве непрерывных вещественных функций, определяемая семейством преднорм
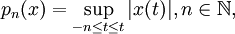 называется топологией компактной сходимости.
называется топологией компактной сходимости. - Топология равномерной сходимости. Пусть на векторном пространстве L(K) непрерывных функций f на компактном топологическом пространстве K определена норма
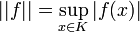 . Топология, порождённая такой метрикой называтеся топологией равномерной сходимости.
. Топология, порождённая такой метрикой называтеся топологией равномерной сходимости. - Точка накопления множества M — точка топологического пространства, в любой проколотой окрестности которой содержится хотя бы одна точка M.
- Точка полного накопления множества M ― точка
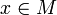 в топологическом пространстве X такая, что пересечение M с любой окрестностью x имеет мощность ту же, что и все множество M.
в топологическом пространстве X такая, что пересечение M с любой окрестностью x имеет мощность ту же, что и все множество M. - Точка прикосновения подмножества M топологического пространства — точка, любая окрестность которой содержит хотя бы одну точку из M. Множество всех точек прикосновения совпадает с замыканием
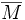 .
.
Ф
Х
- Хаусдорфово пространство. Топологическое пространство X называется хаусдорфовым, если любые две различных точки x и y из X обладают непересекающимися окрестностями.
Литература
- Бурбаки Н. Элементы математики. Общая топология. Основные структуры.
- Александров П. С. Введение в теорию множеств и общую топологию. М.: ГИИТЛ, 1948
- Келли Дж. Л. Общая топология. М.: Наука, 1968
- О. Я. Виро, О. А. Иванов, В. М. Харламов и Н. Ю. Нецветаев. Задачный учебник по топологии
Wikimedia Foundation. 2010.
