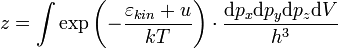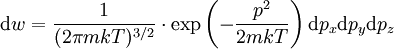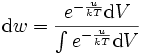Статистика Максвелла — Больцмана

Статистика Максвелла — Больцмана

Статистическая физика

$S = k_B \, \ln\Omega$

Термодинамика Молекулярно-кинетическая теория Статистики Максвелла-Больцмана Бозе-Эйнштейна · Ферми-Дирака Parastatistics · Anyonic statistics Braid statistics Ансамбли Микроканонический · Канонический Большой канонический Изотермо-изобарический Изоэнатльпи-изобарический Термодинамика Уравнение состояния · Цикл Карно · Закон Дюлонга — Пти Модели Модель Дебая · Эйнштейна · Модель Изинга Потенциалы Внутренняя энергия · Энтальпия Свободная энергия Гельмгольца потенциал Гиббса · Большой термодинамический потенциал Известные учёные Максвелл · Гиббс · Больцман

Статистика Максвелла — Больцмана — статистический метод описания физических систем, содержащих большое число невзаимодействующих частиц, движущихся по законам классической механики (то есть классического идеального газа); предложена в 1871 г. австрийским физиком Л. Больцманом.

Вывод распределения

Из общего распределения Гиббса. Рассмотрим систему частиц, находящуюся в однородном поле. В таком поле каждая молекула идеального газа обладает полной энергией

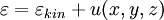$\varepsilon = \varepsilon_{kin} + u(x,y,z)$, где

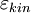$\varepsilon_{kin}$ — кинетическая энергия её поступательного движения, а 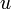$~u$ — потенциальная энергия во внешнем поле, которая зависит от её положения.

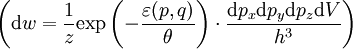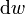Подставим это выражение для энергии в распределение Гиббса для молекулы идеального газа $\left( \mathrm{d} w = \frac{1}{z} \mathrm{exp} \left( - \frac{\varepsilon(p,q)}{ \theta} \right) \cdot \frac{ \mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z \mathrm{d}V}{ h^3} \right)$ (где $~\mathrm{d} w$ — вероятность того, что частица находится в состоянии со значениями координат 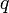$~q$ и импульсов 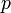$~p$, в интервале $~\mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z \mathrm{d}V$)

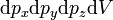имеем:

$\mathrm{d} w = \frac{1}{z h^3} \mathrm{exp} \left(- \frac{ \varepsilon_{kin} + u}{kT} \right) \cdot \mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z \mathrm{d}V$,

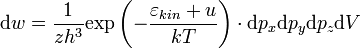где интеграл состояний равен:

$z = \int \mathrm{exp} \left( - \frac{ \varepsilon_{kin} + u}{kT} \right) \cdot \frac{\mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z \mathrm{d}V}{ h^3}$

интегрирование ведется по всем возможным значениям переменных. Далее интеграл состояний можно написать в виде:

$z= \frac{1}{h^3} \int \mathrm{exp} \left(- \frac{ \varepsilon_{kin}}{kT} \right) \cdot \mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z \cdot \int \mathrm{exp} \left(- \frac{{u}}{kT} \right) \mathrm{d}V = \left( \frac{2 \pi m k T}{h^2} \right)^{3/2} \cdot \int \mathrm{exp} \left(- \frac{{u}}{kT} \right) \mathrm{d}V$,

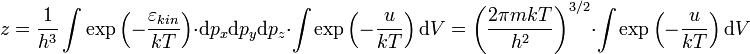мы находим, что нормированное на единицу распределение Гиббса для молекулы газа при наличии внешнего поля имеет вид:

$\mathrm{d} w = \frac{1}{(2 \pi m k T )^{3/2}} \cdot \mathrm{exp} \left(- \frac{{p^2}}{2mkT} \right) \mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z \cdot \frac {e^{- \frac{u}{kT}} \mathrm{d}V} {\int e^{- \frac{u}{kT}} \mathrm{d}V} \qquad\qquad (1)$.

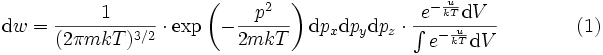Полученное распределение вероятностей, характеризующее вероятность того, что молекула имеет данный импульс и находится в данном элементе объёма, носит название распределение Максвелла — Больцмана.

Некоторые свойства

При рассмотрении распределения Максвелла — Больцмана, бросается в глаза важное свойство — его можно представить как произведение двух множителей:

$\mathrm{d} w = \left[ \frac{1}{(2 \pi m k T )^{3/2}} \cdot \mathrm{exp} \left(- \frac{{p^2}}{2mkT} \right) \mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z \right] \cdot \left[ \frac {e^{- \frac{u}{kT}} \mathrm{d}V} {\int e^{- \frac{u}{kT}} \mathrm{d}V} \right] \qquad\qquad (2)$.

Первый множитель есть не что иное, как распределение Максвелла, оно характеризует распределение вероятностей по импульсам. Второй множитель зависит только лишь от координат частиц и определяется видом её потенциальной энергии. Он характеризует вероятность обнаружения частицы в объёме dV.

Согласно теории вероятности, распределение Максвелла — Больцмана можно рассматривать как произведение вероятностей двух независимых событий — вероятность данного значения импульса и данного положения молекулы. Первая из них:

$\mathrm{d} w = \frac{1}{(2 \pi m k T )^{3/2}} \cdot \mathrm{exp} \left(- \frac{{p^2}}{2mkT} \right) \mathrm{d}p_x \mathrm{d}p_y \mathrm{d}p_z$

представляет распределение Максвелла; вторая вероятность:

$\mathrm{d} w = \frac {e^{- \frac{u}{kT}} \mathrm{d}V} {\int e^{- \frac{u}{kT}} \mathrm{d}V}$

— распределение Больцмана. Очевидно, что каждое из них нормировано на единицу.

Распределение Больцмана является частным случаем канонического распределения Гиббса для идеального газа во внешнем потенциальном поле, так как при отсутствии взаимодействия между частицами распределение Гиббса распадается на произведение распределений Больцмана для отдельных частиц.

Независимость вероятностей дает важный результат: вероятность данного значения импульса совершенно не зависит от положения молекулы и, наоборот, вероятность положения молекулы не зависит от её импульса. Это значит что распределение частиц по импульсам (скоростям) не зависит от поля, другими словами остается тем же самым от точки к точке пространства, в котором заключен газ. Меняется лишь вероятность обнаружения частицы или, что то же самое, число частиц.

См. также

• Статистика Бозе — Эйнштейна
• Статистика Ферми — Дирака
• Распределение Максвелла
• Распределение Гиббса