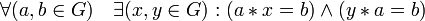Группа (алгебра)

Гру́ппа — в абстрактной алгебре непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Ветвь математики, занимающаяся группами, называется теорией групп.

Всем знакомые вещественные числа наделены сложением — операцией, обладающей некоторым набором свойств. Похожими свойствами обладают и многие другие из объектов, которые изучает математика, — например, множество вращений плоскости вокруг начала координат. Теория групп занимается изучением взаимосвязей между этими свойствами в общем виде. Структура группы включается в различные другие алгебраические структуры, такие как поля, векторные пространства или группы Ли. Кроме того, группы являются важными инструментами в изучении симметрии во всех её проявлениях.

Определения

Непустое множество G с заданной на нём бинарной операцией 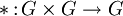$\,*\,\colon G \times G \to G$ называется группой (G, * ), если выполнены следующие аксиомы:

1. ассоциативность: $\forall (a, b, c\in G): (a*b)*c = a*(b*c)$;
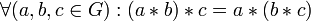2. наличие нейтрального элемента: $\exists e \in G \quad \forall a \in G:(e*a=a*e=a)$;
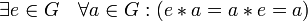3. наличие обратного элемента: $\forall a \in G \quad \exists a^{-1}\in G: (a*a^{-1}=a^{-1}*a=e)$

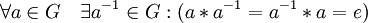
Комментарии

• Заметим, что от группы не требуется свойства a * b = b * a (так называемой коммутативности).
  • Пары элементов, для которых это равенство выполнено, называются перестановочными или коммутирующими.
  • Множество элементов, перестановочных со всеми элементами группы, называется центром группы.
  • Группа, для которой это равенство выполнено для произвольных элементов 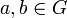$a, b\in G$, называется коммутативной, или абелевой.
• В определении группы 2-ю и 3-ю аксиомы можно заменить одной аксиомой существования обратной операции:

$\forall (a,b\in G) \quad \exists (x,y\in G): (a*x=b)\and (y*a=b)$

• Вышеприведённые аксиомы не являются строго минимальными. Для существования нейтрального и обратного элементов достаточно наличия левого нейтрального (e_l * a = a) и левого обратного (a' * a = e_l) элементов. При этом они автоматически являются e и a ^{- 1}:

$e_l = a'*a \Leftrightarrow e_l*e_l = a'*a \Leftrightarrow a'*a*e_l = a'*a \Leftrightarrow a''*a'*a*e_l = a''*a'*a \Leftrightarrow$

$\Leftrightarrow e_l*a*e_l = e_l*a \Leftrightarrow a*e_l = a$;

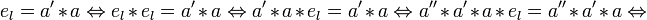
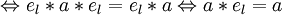a * a' = e * (a * a') = (a'' * a') * (a * a') = a'' * (e * a') = a'' * a' = e.

Связанные определения

см. основую статью Словарь терминов теории групп.

• Подгруппа — подмножество H группы G, которое является группой относительно операции, определённой в G.
• Порядок группы (G, * ) — мощность G (т. е. число её элементов).
  • Если множество G конечно, то группа называется конечной.

Примеры

• Целые числа с операцией сложения. 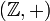$(\Z,+)$ группа с нейтральным элементом 0. Она является абелевой.

• Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность и единица.

• Свободная группа с двумя образующими (F₂) состоит из пустого слова, которое мы обозначаем $\varepsilon$ (это единица нашей группы), и всех конечных слов из четырёх символов a,a ^{− 1},b и b ^{- 1} таких, что a не появляется рядом с a ^{- 1} и b не появляется рядом с b ^{- 1}. Операция умножения таких слов — это просто соединение (конкатенация) двух слов в одно с последующим сокращением пар aa ^{− 1},a ^{− 1}a,bb ^{− 1} и b ^{− 1}b.

• Симметрическая группа. Множество всех биекций конечного множества в себя с операцией композиции является конечной некоммутативной группой, которая называется симметрической группой, или группой перестановок. Любая конечная группа является подгруппой некоторой симметрической группы (теорема Кэли).

• Циклические группы состоят из степеней 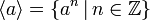$\langle a\rangle = \{a^n \,| \,n \in \mathbb{Z}\}$ одного элемента a. Такие группы всегда коммутативны. Примеры таких групп — упомянутые уже целые числа по сложению и группа корней из единицы.

Стандартные обозначения

Мультипликативная запись

Обычно групповую операцию называют (абстрактным) умножением; тогда применяется мультипликативная запись:

• результат операции называют произведением и записывают a * b или ab;
• нейтральный элемент обозначается «1» и называется единицей;
• обратный к a элемент записывается как a ^{- 1}.

Кратные произведения 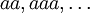$aa, aaa,\dots$ записывают в виде целых степеней 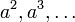$a^2, a^3,\dots$, причём (a ^{− 1})ⁿ = a ^{− n},a⁰ = e.

Аддитивная запись

В коммутативной группе определяющяя операция часто рассматривается как (абстрактное) сложение и записывается аддитивно:

• пишут «a + b» и называют получившийся элемент суммой элементов a и b;
• обозначают нейтральный элемент «0» и называем его нулём;
• обратный элемент к a обозначают как «−a» и называют его противоположным к a элементом;
• запись сокращают следующим образом: a + (-b) = a - b;
• выражения вида a + a, a + a + a, -a - a, … обозначают символами 2a, 3a, -2a, …

Простейшие свойства

• Обратный к данному элемент всегда определяется однозначно.
• (a^-1)^-1 = a, a^maⁿ = a^m+n, (a^m)ⁿ = a^mn.
• (ab)^-1 = b^-1a^-1.
• Верны законы сокращения:

$c \cdot a = c \cdot b \Leftrightarrow a = b$,

$a \cdot c = b \cdot c \Leftrightarrow a = b$.

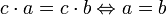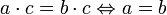• Обратный элемент к нейтральному есть сам нейтральный элемент.
• Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление».
• Пересечение двух подгрупп группы G есть подгруппа группы G.
• Теорема Лагранжа: если G — группа конечного порядка g, то порядок g₁ любой её подгруппы G₁ является делителем порядка группы. Из этого следует, что и порядок любого элемента делит порядок группы.

Получение новых групп из уже известных

• В группе может существовать несколько подгрупп. Для определения их числа пользуются теоремой Лагранжа и теоремами Силова.
• Пусть дана группа G и её нормальная подгруппа H, тогда факторгруппа G/H есть множество смежных классов по H вместе с операцией умножения, которая корректно определяется по представителям: (gH)(hH)=(gh)H.
• Полупрямое произведение и, в частности,
  • Прямое произведение двух групп (G,·) и (H,•) есть множество G×H пар, наделённое операцией покомпонентного умножения: (g₁,h₁)(g₂,h₂) = (g₁ · g₂,h₁•h₂).
• Свободное произведение двух групп G и H есть группа, система образующих которой есть объединение систем образующих G и H, a система соотношений есть объединение систем соотношений G и H. Например, модулярная группа является свободным произведением 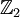$\Z_2$ и $\Z_3$.

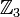Обобщения

• Группоид — магма.
• Полугруппа
• Множество G с заданной на нём бинарной операцией ·, удовлетворяющее только первым двум аксиомам, называется моноидом. Таким образом, группа может быть определена как моноид, в котором каждый элемент обратим.
• Квазигруппа

См. также

• Алгебраические структуры
• Словарь терминов теории групп
• Группа многогранника
• Группа Клейна

Популярная литература

• Александров П. С. Введение в теорию групп, выпуск 7 серии «Библиотечка Квант».
• Садовский Л., Аршинов М., Группы, Квант, №10, 1976.

Научная литература

• Белоногов В. А. Задачник по теории групп. М.: Наука, 2000.
• Каргаполов М. И., Мерзляков Ю. И. Основы теории групп. М.: Наука, 1982.
• Кострикин А. И. Введение в алгебру. М.: Наука, 1977.
• Курош А. Г. Теория групп. (3-е изд.). М.: Наука, 1967.
• Холл М. Теория групп. М.: Издательство иностранной литературы, 1962.
• Gorenstein D. Finite groups. N.Y.: Harper and Row, 1968.
• Huppert B. Endliche Gruppen. I.B.: Springer, 1967.

Ссылки