Свободная группа

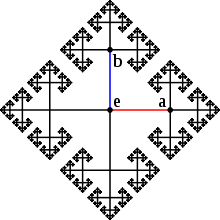Граф Кэли свободной группы образованной двумя элементами a и b

В математике, а именно, в теории групп, группа $G$ называется свобо́дной гру́ппой, если существует подмножество $S$ в $G$, такое что каждый элемент $G$ записывается единственным образом как произведение конечного числа элементов $S$ и их обратных. (Единственность понимается с точностью до тривиальных комбинаций наподобие $st=su^{-1}ut$.) Говорят, что $G$ (свободно) порождена $S$ и пишут: $F_S$ или $F_n,$ если $S$ есть множество из $n$ элементов.

Близкое, но отличное понятие: свободная абелева группа (которая не является, вообще говоря, свободной группой).

Явная конструкция

Для формального понятия, которое обсуждалось выше, можно предъявить явную конструкцию (доказав тем самым существование свободных групп)^[1][2]. Будем считать элементы множества $S$ «символами» и для каждого символа $s$ из $S$ введём символ $s^{-1};$ множество последних обозначим $S^{-1}$. Пусть

$T = S \cup S^{-1}.$

Определим слово над $S$ как конечную цепочку (возможно, повторяющихся) символов из $T,$ записанных друг за другом. Вместе с операцией конкатенации (склейки, приписывания) множество слов над $S$ становится полугруппой. Будем считать, что во множестве слов имеется пустое слово $\varepsilon$, которое не содержит символов. Таким образом получается моноид слов над $S.$

Пример. $S = \{a, b, c\}$. $T = \{a, a^{-1}, b, b^{-1}, c, c^{-1}\}$. Два слова,

$\scriptstyle \alpha = abc^{-1}a, ~~ \beta = b^{-1}ba^{-1}.$

Их конкатенация:

$\scriptstyle \gamma = \alpha\beta = abc^{-1}ab^{-1}ba^{-1}.$

Напомним, что, к примеру, $\scriptstyle \alpha\varepsilon = \alpha = abc^{-1}a.$

Введём теперь правило редукции слов. Если в некотором слове за символом (символу) из $S$ следует (предшествует) соответствующий ему символ из $S^{-1},$ то удаление этой пары символов назовём редукцией. Слово называется редуцированным, если в нём больше нельзя провести редукцию. Полной редукцией называется последовательное применение редукции к данном слову до тех пор, пока оно не станет редуцированным. Например, из слова $\gamma$ (см. пример выше) после полной редукции получается редуцированное слово: $abc^{-1}.$

Свободной группой $F_S,$ порождённой множеством $S,$ (короче, свободной группой над $S$) называется группа редуцированных слов над $S$ с операцией конкатенации (за которой следует полная редукция результата при необходимости).

Свойства

• Все свободные группы, порождённые равномощными множествами, изоморфны. При этом мощность множества, порождающего данную свободную группу, называется её рангом.
• Свободная группа $F_n$ изоморфна свободному произведению $n$ копий $\Z$.
• Теорема Нильсена — Шрайера: любая подгруппа свободной группы свободна.
• Любая группа $G$ есть факторгруппа некоторой свободной группы $F_S$ по некоторой её подгруппе H. За $S$ могут быть взяты образующие $G$. Тогда существует естественный эпиморфизм $f:\;F_S \to G$. Ядро H этого эпиморфизма является множеством соотношений задания $G = \langle S, H \rangle$.
• Коммутант свободной группы конечного ранга имеет бесконечный ранг. Например, коммутант порождённой двумя элементами свободной группы $F(a,b)$ — это свободная группа, порождённая всеми коммутаторами $[a^n, b^m],$ $m,n\ne 0.$

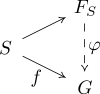
Универсальность

Свободная группа $F_S$ — это в некотором смысле наиболее общая группа, порождённая множеством $S.$ А именно, для любой группы $G$ и любого отображения множеств $f\colon S \to G$ существует единственный гомоморфизм групп $\varphi\colon F_S \to G,$ для которого следующая диаграмма коммутативна:

Таким образом, существует взаимно однозначное соответствие между множествами отображений $S \to G$ и гомоморфизмов $F_S \to G.$ Для несвободной группы соотношения в группе накладывали бы ограничения на возможные образы образующих элементов группы.

Указанное выше свойство можно принять за определение свободной группы^[3], при этом она определена лишь с точностью до изоморфизма, как и любой универсальный объект. Это свойство называется универсальностью свободных групп. Порождающее множество $S$ называется базисом группы $F_s.$ Одна и та же свободная группа может иметь разные базисы.

С точки зрения теории категорий, свободная группа — это функтор из категории левым сопряжённым для забывающего функтора $\bold{Grp} \to \bold{Set}.$

Примечания

1. ↑ Линдон Р., Шупп П. Комбинаторная теория групп. — М.: Мир, 1980. — С. 13.
2. ↑ Гл. 5, § 14 // Основы теории групп / Каргаполов М.И., Мерзляков Ю.И. — 3-е изд. — М.: Наука, 1982. — 288 с.
3. ↑ С. Маклейн Категории для работающего математика, — М.: Физматлит, 2004. — 352 с — ISBN 5-9221-0400-4.

Литература

• Гл. II, 1.2 // Общая алгебра / Под общей редакцией Л.А. Скорнякова. — М.: Наука. Гл. ред. физ.-мат. лит., 1990. — Т. 1. — 592 с.