Формулы аналогии Непера

Сферический треугольник.

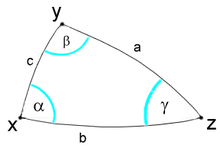
Формулы аналогии Непера в сферической тригонометрии выражают соотношения между пятью элементами сферического треугольника, удобные для решения косоугольного сферического треугольника по двум сторонам и углу между ними и по двум углам и прилежащей к ним стороне.

Описание

Формулы аналогии Непера имеют следующий вид^[1]:

$~\operatorname{tg}\frac{\alpha+\beta}{2}= \frac{\cos\frac{a-b}{2}}{\cos\frac{a+b}{2}}\cdot\operatorname{ctg}\frac{\gamma}{2}$

$~\operatorname{tg}\frac{\alpha-\beta}{2}= \frac{\sin\frac{a-b}{2}}{\sin\frac{a+b}{2}}\cdot\operatorname{ctg}\frac{\gamma}{2}$

$~\operatorname{tg} \frac{a+b}{2}= \frac{\cos\frac{\alpha-\beta}{2}}{\cos\frac{a+b}{2}}\cdot\operatorname{tg}\frac{c}{2}$

$~\operatorname{tg} \frac{a-b}{2}= \frac{\sin\frac{\alpha-\beta}{2}}{\sin\frac{a+b}{2}}\cdot\operatorname{tg}\frac{c}{2}$

Эти формулы считаются более удобными для решения косоугольных сферических треугольников по двум сторонам и углу между ними и по двум углам и прилежащей к ним стороне, чем формулы Деламбра. Хотя каждая из них выводится простым делением правой и левой частей одной формулы Деламбра на соответствующие части другой.

При решении косоугольного сферического треугольника по двум сторонам и углу между ними из первой и второй формул получают углы $\alpha\,$ и $\beta\,$, а затем сторону $c\,$ находят из третьей или четвёртой формулы. При решении косоугольного сферического треугольника по двум углам и прилежащей к ним стороне из третьей и четвертой формул получают стороны $a\,$ и $b\,$, а затем угол $\gamma\,$ находят из первой или второй формулы.

Примечания

1. ↑ Степанов Н. Н. §42. Формулы «аналогии Непера» // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 87-90. — 154 с.

Ссылки

• Формулы аналогии Непера на сайте MathWorld