Сферическая теорема Пифагора

Прямоугольный сферический треугольник с гипотенузой c, катетами a и b и прямым углом C.

Сферическая теорема Пифагора — теорема, устанавливающая соотношение между сторонами прямоугольного сферического треугольника.

Формулировка и доказательство

Сферическая теорема Пифагора формулируется следующим образом^[1]:

Косинус гипотенузы прямоугольного сферического треугольника равен произведению косинусов его катетов.

Рисунок к доказательству сферической теоремы Пифагора.

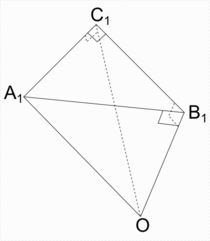
Доказательство проведём с помощью трёхгранного угла^[1] OA₁B₁C₁ со сторонами (лучами) OA₁, OB₁, OC₁ и вершиной в точке O, плоские углы A₁OC₁ и C₁OB₁ которого равны катетам b и a данного треугольника, плоский угол A₁OB₁ равен его гипотенузе c, двугранный угол между гранями A₁OC₁ и C₁OB₁ равен 90 градусов, а остальные два двугранных угла равны соответствующим углам сферического прямоугольного треугольника. Этот трёхгранный угол пересечен плоскостью A₁B₁C₁, перпендикулярной лучу OB₁. Тогда углы A₁C₁O и A₁C₁B₁ будут прямыми.

Заметим, что

$\frac {OB_1}{OA_1} = \cos \angle A_1OB_1 = \cos c,\,$

$\frac {OC_1}{OA_1} = \cos \angle A_1OC_1 = \cos b,\,$

$\frac {OB_1}{OC_1} = \cos \angle C_1OB_1 = \cos a.\,$

Отсюда

$\cos c = \frac {OB_1}{OA_1} = \frac {OB_1}{OC_1} \cdot \frac {OC_1}{OA_1} = \cos a \cos b.\,$

Что и требовалось доказать.

Если считать, что сферическая теорема косинусов уже доказана, формулу для сферической теоремы Пифагора можно сразу получить из неё, записав сферическую теорему косинусов для гипотенузы данного прямоугольного сферического треугольника и просто подставив в получившееся выражение угол 90 градусов, косинус которого равен нулю.

Следствия и применение

При радиусе сферы, стремящемся к бесконечности, сферическая теорема Пифагора переходит в теорему Пифагора планиметрии. Поэтому, поскольку радиус Земли велик, при небольших расстояниях прямоугольные треугольники на поверхности Земли (например, используемые для измерения расстояний и углов на местности) практически подчиняются теореме Пифагора планиметрии^[2], тогда как для больших расстояний, сравнимых с радиусом Земли, уже необходимо применять сферическую теорему Пифагора.

С применением сферической теоремы Пифагора можно получить формулы для разности долгот и расстояния между точками земной поверхности, а, следовательно, и соответствующие формулы для расстояний и координат точек на небесной сфере.

Из сферической теоремы Пифагора следует, что в прямоугольном сферическом треугольнике количество сторон, меньших 90 градусов, нечётно, а больших — чётно^[1]. Поэтому если оба катета прямоугольного сферического треугольника больше 90 градусов, то его гипотенуза меньше 90 градусов, то есть в этом случае гипотенуза короче каждого из двух катетов — положение, невозможное для прямоугольного треугольника на плоскости.

История

Сферическая теорема Пифагора была известна ещё Ал-Бируни, который вместе с тем не знал сферической теоремы косинусов, поэтому применил сферическую теорему Пифагора и теорему синусов для решения как минимум двух задач: определения разности долгот двух пунктов на поверхности Земли по их широтам и расстоянию между ними и определения расстояния между двумя пунктами на поверхности Земли по их широтам и долготам^[3]:81.

См. также

• Теорема Пифагора

Примечания

1. ↑ ^{1 2 3} Степанов Н.Н. Сферическая теорема Пифагора // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 42—44. — 154 с.
2. ↑ John McCleary Geometry from a differentiable viewpoint. — Cambridge University Press, 1994. — С. 6. — 308 с.
3. ↑ Розенфельд Б.А., Рожанская М.М. Астрономический труд Ал-Бируни «Канон Мас'уда» // Историко-астрономические исследования. — М.: Наука, 1969. — В. X. — С. 63—96.