Закон Мерсенна

Колебания струн пианино описываются дифференциальными уравнениями

Спор о струне́ (также спор о коле́блющейся струне́, спор о звуча́щей струне́) — научная дискуссия, развернувшаяся в XVIII веке между математиками вокруг изучения колебаний струны. Дискуссия касалась определения понятия функции и оказала решающее влияние на множество разделов математики: теорию дифференциальных уравнений в частных производных, математический анализ и теорию функций вещественного переменного, теорию тригонометрических рядов Фурье и теорию обобщенных функций и пространств Соболева.

Предпосылки к спору

Марин Мерсенн, французский богослов, философ, математик и теоретик музыки

Возможность теоретического изучения колебаний с точки зрения механики появилась с открытием законов Ньютона (1687) и разработкой анализа бесконечно малых, интегрального и дифференциального исчислений. Однако, экспериментальные исследования велись до этого момента Галилеем, Мерсенном, Декартом, Гюйгенсом и др. В 1625 году Мерсеном была обнаружена зависимость между частотой ν, натяжением T, площадью поперечного сечения A и длиной l струны, выражающаяся в пропорциональности

$\nu \propto \frac{1}{l}\sqrt{\frac{T}{A}}$

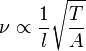
Закон Мерсена был выведен из математических соображений Тейлором почти через столетие, в 1713 году. В его работе исследуется отклонение струны от начального положения, выраженное в виде функции y = y(x).

Тейлор полагал, что в любой фиксированный момент времени струна должна иметь форму синусоиды y = asin(kπx / l) (что на самом деле оказывается простейшей формой колеблющейся струны), амплитуда которой зависит от времени, и что при любом начальном условии струна стремится перейти в такое «основное» состояние (что, как оказалось, не соответствует действительности). Этот подход, иногда называемый «методом стоячих волн», был продолжен Д. Бернулли, однако получил строгое обоснование лишь в работах Фурье.

Тейлор также установил, что сила натяжения, действующая на бесконечно-малый элемент струны и направленная в сторону её отклонения, пропорциональна второй производной d²y / dx². В дальнейшем Д’Аламбер стал рассматривать зависимость отклонения не только от пространственной координаты x, но и от времени t. Это позволило строго применить второй закон Ньютона, что, однако, потребовало переосмысления природы производной, рассматриваемой Тейлором: она стала частной производной 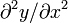$\partial^2 y/\partial x^2$. Ускорение элемента описывалось другой частной производной: $\partial^2 y/\partial t^2$.

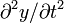В 1747 году Д’Аламбер переформулировал закон, найденный Тейлором, в терминах дифференциальных уравнений с частными производными и записал уравнение колебания струны в современном виде (изменяя масштаб времени, можно положить a = 1, что и будет делаться в дальнейшем):

$\frac{\partial^2 y}{\partial t^2}=a^2 \frac{\partial^2 y}{\partial x^2}.$

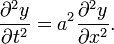
Исследование этого уравнения привело к «методу бегущих волн», представляющего собой другой взгляд на проблему колебательного движения. Впоследствии он был развит Эйлером. С тех пор это уравнение заняло прочное место в учебниках по математике, математической физике, теории колебаний, а также других математических дисциплин и по сути стало считаться классическим.

Метод бегущих волн

Жан Лерон Д’Аламбер, французский философ, механик и математик

Леонард Эйлер, выдающийся математик XVIII века

Д’Аламбер применяет следующий подход к решению уравнения колебания струны. Он замечает, что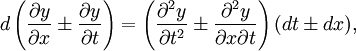

$d\left( \frac{\partial y}{\partial x}\pm \frac{\partial y}{\partial t} \right)=\left( \frac{\partial^2y }{\partial t^2}\pm \frac{\partial^2 y}{\partial x\partial t}\right)(dt\pm dx),$

и делает вывод, что коэффициент при дифференциальной форме 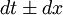$dt\pm dx$ является функцией от 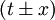$(t\pm x)$ и может быть вычислен интегрированием правой части этого равенства. Это позволяет записать линейную систему на первые частные производные от 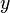$y\quad$, решение которой даёт полный дифференциал функции 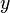$y\quad$. Последняя восстанавливается повторным интегрированием. Этот метод позволяет записать решение уравнения колебания струны в виде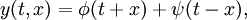

$y(t,x)=\phi(t+x)+\psi(t-x), \quad$

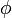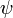где $\phi\quad$ и $\psi\quad$ — некоторые произвольные функции, определяемые из начальных условий. Д’Аламбер назвал такое решение общим, подчеркивая, что оно представляет собой целое множество различных решений уравнения.

Аналогичное решение вскоре получил Эйлер, сформулировав то, что мы сейчас назвали бы задачей Коши с заданной начальной формой струны и нулевой начальной скоростью. Рассматривая уравнение колебания струны для произвольного 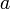$a\quad$, он получает решение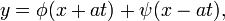

$y=\phi(x+at)+\psi(x-at), \quad$

незначительно отличающееся от решения Д’Аламбера. В 1766 году Эйлер разрабатывает новый метод, известный сейчас как метод характеристик: переходя к координатам 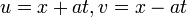$u=x+at, v=x-at\quad$, он записывает исходное уравнение в виде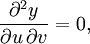

$\frac{\partial^2y}{\partial u\, \partial v}=0,$

который легко поддается интегрированию.

Несмотря на то, что Д’Аламбер и Эйлер получили по сути одинаковые решения уравнения колебания, они очень по-разному воспринимали их смысл. Заметим, что к этому моменту в математике не было общепринятого определения функции и современных понятий непрерывности и гладкости, а среди математиков существовали разные мнения о том, какие функции следует рассматривать в анализе, а какие нет. Неопределённость в общем решении уравнения колебания струны остро поставила этот вопрос на повестку дня математического сообщества того времени, причём Эйлер и Д’Аламбер оказались здесь по разные стороны баррикад.

Определение функции

Исаак Барроу, английский математик, физик и богослов, учитель Ньютона

В зарождающемся математическом анализе XVII—XVIII веков присутствовали два основных подхода: наглядный и нестрогий механико-геометрический и формальный алгебраический. С этих двух точек зрения воспринималось и понятие функции. С механистической точки зрения, восходящей к Ньютону и Барроу, функция — это переменная величина, изменяющаяся с течением времени. Последнее в данном случае выступает в качестве аргумента. Другой подход к функции, впервые четко сформулированный И. Бернулли, состоит в том, что «функцией переменной величины… называется количество, составленное каким угодно способом из этой переменной величины и постоянных», то есть, некоторая формула, аналитическое выражение от аргумента (не обязательно являющееся аналитической функцией в современном понимании). Класс допустимых операций, с помощью которых можно было получать функции, также варьировался, однако обычно включал в себя арифметические действия, извлечение корня и переходы к пределам, что позволяло рассматривать бесконечные ряды.

Вопрос об этих двух подходах к функции и стал ключевым в споре о звучащей струне — сначала между Эйлером и Д’Аламбером, а затем и другими математиками.

Понятно, что с механической точки зрения струна в начальный момент времени может иметь форму практически произвольной (непрерывной в современном понимании, возможно гладкой) кривой. С связи с этим Эйлер предлагал считать, что начальное условие (а, следовательно, и решение) может быть задано не одним аналитическим выражением, а несколькими («кусочно-аналитическое» задание), а впоследствии и вообще отказался от аналитического задания.

Д’Аламбер же считал, что рассматривать произвольную кривую нельзя — сама постановка уравнения колебания требует, чтобы решение имело как минимум вторые частные производные (было дважды дифференцируемым). В то же время, одно из распространённых мнений того времени заключалось в том, что гладкая кривая может быть задана только одной аналитической формулой (считалось, что две функции, заданные аналитическими формулами и совпадающие на каком-то участке, должны совпадать везде), и наоборот — аналитическая формула задаёт только гладкие на своей области определения функции. Как будет ясно позднее, оба этих соображения не соответствуют действительности.

Особую роль здесь сыграло и свойство гиперболических уравнений в частных производных (к которым относится волновое) сохранять гладкость начального условия, а не увеличивать её (что происходит в случае эллиптических уравнений), а также наглядные представления о струне, отклонённой в небольшой области, форма которой имеет негладкие «изломы». Парадокс заключался в том, что формула, найденная Д’Аламбером и Эйлером, была осмысленна даже в том случае, когда само уравнение не имело смысла во всех точках (в случае негладких функций).

Метод стоячих волн

Идея о важной роли «чистых колебаний» синусоидальной формы, появившаяся еще у Тейлора, была развита Д. Бернулли. Его догадка заключалась в том, что произвольное колебание может быть представлено как «наложение» или сумма нескольких чистых колебаний, что соответствовало наблюдением за струной: издаваемый ею звук состоит из основного тона и множества обертонов. Бернулли нашёл решение уравнения колебания в виде суммы тригонометрического ряда и утверждал, исходя из физических соображений, что произвольная функция может быть выражена таким рядом.

Ряды были важным объектом изучения в то время, и многие математики (включая Ньютона) рассматривали степенные ряды (с вещественными показателями степеней) как универсальный способ записи произвольных функций. Однако, необходимого уровня понимания тригонометрического ряда на тот момент достигнуто не было, и ни Д’Аламбер, ни Эйлер не согласились с тем, что тригонометрический ряд способен описывать достаточно широкий класс функций. Например, возражения вызывало требование периодичности к такой функции, естественно следующее из периодичности слагаемых. Эйлер также не мог поверить в то, что тригонометрическим рядом можно описать поведение струны, возмущённой только на небольшом участке. Лишь в работах Фурье было показано, что даже недоступная для описания степенным рядом (и не являющаяся аналитической в современном понимании) функция вида y = | x | может быть представлена тригонометрическим рядом. Дальнейшие исследования вопросов сходимости рядов Фурье привели Кантора к построению теории множеств и, в конечном итоге, к появлению современного функционального анализа.

Обобщённые функции

Однако, окончательная точка в споре о струне не была поставлена с появлением современного теоретико-множественного подхода к понятию функции как к отображению. Парадокс, связанный с возможностью негладкости начальных условий, а, следовательно, и решений, был разрешён только в XX веке с появлением аппарата обобщённых функций (распределений). Основы этой теории были заложены в конце 1936 году С.Л. Соболевым в результате исследований задачи Коши для гиперболических уравнений (к которым, напомним, относится и уравнение колебания струны) и в дальнейшем строго развиты Лораном Шварцом (Laurent Schwartz) в 1950-х годах.

Идея состоит в замене уравнения колебания на эквивалентное ему (в некотором смысле) интегральное уравнение, решение которого ищется уже не в классе дважды гладких функций, а в так называемых Соболевских пространствах, представляющих собой пополнение пространства непрерывных функций по некоторой специальной метрике. Можно также считать, что производные негладкой функции, стоящие в левой части уравнения колебания струны, являются обобщённой функцией, и равенство справедливо в смысле обобщённых функций.

Литература

• 1. История математики с древнейших времен до начала XIX столетия. — Под ред. А. П. Юшкевича. — Т. 1—3. М.: Наука. 1970—1972.
• 2. Дж. Стиллвелл, Математика и ее история. — Ижевск: Институт компьютерных исследований/РХД, 2004. — 530 с.
• 3. Большая Советская Энциклопедия, статья «Функция»