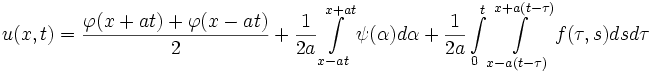Уравнение колебания струны
- Уравнение колебания струны
-
Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн.
Вид уравнения
В общем случае волновое уравнение записывается в виде
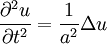 ,
,
где 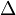 — оператор Лапласа,
— оператор Лапласа, 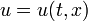 — неизвестная функция,
— неизвестная функция, 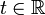 — время,
— время, 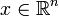 — пространственная переменная.
— пространственная переменная.
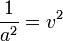 ,
,
где 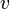 — фазовая скорость.
— фазовая скорость.
В одномерном случае уравнение называется также уравнением колебания струны и записывается в виде
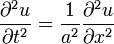 .
.
Оператор Д’Аламбера
Разность 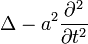 называется оператором Д’Аламбера (разные источники используют разный знак). Таким образом, волновое уравнение записывается как:
называется оператором Д’Аламбера (разные источники используют разный знак). Таким образом, волновое уравнение записывается как: 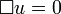
Неоднородное уравнение
Допустимо также рассматривать неоднородное волновое уравнение
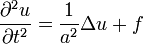 ,
,
где f = f(x,t) — некая заданная функция внешнего воздействия (внешней силы).
Стационарным вариантом волнового уравнения является уравнение Лапласа (уравнение Пуассона в неоднородном случае).
Задача нахождения нормальных колебаний системы, описываемой волновым уравнением, приводит к задаче на собственные значения для уравнения Лапласа, то есть к нахождению решений уравнения Гельмгольца, получающегося подстановкой
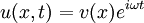 или
или 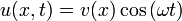 .
.
Решение волнового уравнения
-
Существует аналитическое решение гиперболического уравнения в частных производных. В евклидовом пространстве произвольной размерности оно называется формулой Кирхгофа. Частные случаи: для колебания струны (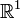 ) — формула Д’Аламбера, для колебания мембраны (
) — формула Д’Аламбера, для колебания мембраны (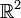 ) — формула Пуассона.
) — формула Пуассона.
Решение одномерного волнового уравнения
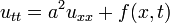 (функция f(x,t) соответствует вынуждающей внешней силе)
(функция f(x,t) соответствует вынуждающей внешней силе)
с начальными условиями

имеет вид
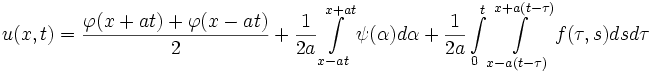
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Уравнение колебания струны" в других словарях:
Уравнение колебаний струны — Волновое уравнение в математике линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика,… … Википедия
Уравнение в частных производных — Дифференциальное уравнение в частных производных (общеупотребительно сокращение (Д)УЧП, также известны как уравнения математической физики, УМФ) дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные… … Википедия
Дифференциальное уравнение в частных производных — (частные случаи также известны как уравнения математической физики, УМФ) дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные. Содержание 1 Введение 2 История … Википедия
Дифференциальное уравнение с частными производными — Дифференциальное уравнение в частных производных (общеупотребительно сокращение (Д)УЧП, также известны как уравнения математической физики, УМФ) дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные… … Википедия
ЛИНЕЙНОЕ ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ И СИСТЕМА — дифференциальное уравнение (и система) с частными производными вида у к poro в любой точке х=( х 0, x1 . . ., х n).области его задания среди действительных переменных y0, y1 . . ., yn можно выделить (в случае надобности после надлежащего… … Математическая энциклопедия
Волновое уравнение — в математике линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно… … Википедия
Волновое уравнение — дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде. В случае малых возмущений и однородной изотропной среды В. у. имеет вид: где х, у, z пространственные… … Большая советская энциклопедия
волновое уравнение — дифференциальное уравнение с частными производными 2 го порядка, описывающее процесс распространения возмущений в некоторой среде. Например, малые колебания натянутой струны описываются волновым уравнением ,где u (х, t) искомая функция … … Энциклопедический словарь
ШРЕДИНГЕРА УРАВНЕНИЕ — основное динамич. ур ние нерелятив. квант. механики; предложено австр. физиком Э. Шрёдингером (Е. Schr?dinger) в 1926. В квант. механике Ш … Физическая энциклопедия
Шрёдингера уравнение — основное динамическое уравнение нерелятивистской квантовой механики (См. Квантовая механика); названо в честь австрийского физика Э. Шрёдингера, который предложил его в 1926. В квантовой механике Ш. у. играет такую же фундаментальную роль … Большая советская энциклопедия
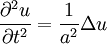 ,
,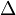 — оператор Лапласа,
— оператор Лапласа, 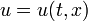 — неизвестная функция,
— неизвестная функция, 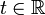 — время,
— время, 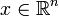 — пространственная переменная.
— пространственная переменная.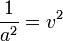 ,
,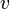 — фазовая скорость.
— фазовая скорость.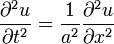 .
.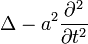 называется оператором Д’Аламбера (разные источники используют разный знак). Таким образом, волновое уравнение записывается как:
называется оператором Д’Аламбера (разные источники используют разный знак). Таким образом, волновое уравнение записывается как: 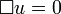
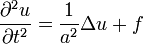 ,
,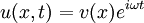 или
или 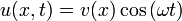 .
.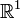 ) — формула Д’Аламбера, для колебания мембраны (
) — формула Д’Аламбера, для колебания мембраны (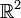 ) — формула Пуассона.
) — формула Пуассона.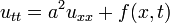 (функция f(x,t) соответствует вынуждающей внешней силе)
(функция f(x,t) соответствует вынуждающей внешней силе)