Коалгебра

Коалгебра - математическая структура, которая двойственна (в смысле обращения стрелок) к унитарной ассоциативной алгебре. аксиомы унитарной ассоциативной алгебры могут быть сформулированы в терминах коммутативных диаграмм. Аксиомы коалгебры получаются путём обращения стрелок. Каждая коалгебра c дуальностью (векторного пространства) порождает алгебру, но не наоборот. В конечномерном случае дуальность есть в обеих направлениях. Коалгебры встречаются в разных случаях (например, универсальных обёртывающих алгебрах и схемах групп). Существует также F-коалгебра, с важными приложениями в компьютерных науках.

Определение

Коалгебра над полем K есть векторное пространство C над K вместе с тензорное произведение над K.)

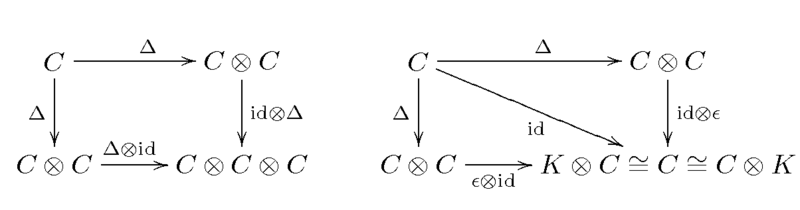
Равносильно, следующие две диаграммы коммутируют:

На первой диаграмме мы отождествляем $C\otimes (C\otimes C)$ с $(C \otimes C)\otimes C$ как два естественно изоморфных пространства.^[1] Аналогично, на второй диаграмме отождествлены естественно изоморфные пространства $C$ , $C\otimes K$ и $K\otimes C$.^[2]

Первая диаграмма дуальна диаграмме, выражающей ассоциативность операции умножения алгебры (называется коассоциативность коумножения); вторая диаграмма дуальна диаграмме, выражающей существования мультипликативного нейтрального элемента (единицы по операции умножения). Соответственно, отображение Δ называется коумножение (или копроизведение) C и ε является коединицей C.

Пример

Обозначим множество S и образуем K-векторное пространство с базисом S. Элементами этого векторного пространства являются такие функции из S в K которые отображают все но ограниченно многие элементы из S к нулю; мы отождествим элемент s из S с функцией которая отображает s в 1 и все остальные элементы S в 0. Мы будем обозначать это пространство как C. Мы определим

$\Delta(s) = s\otimes s \quad \mbox{ and } \quad \epsilon(s)=1 \quad \mbox{ for all } s\in S.$

Благодаря линейности, Δ и ε могут быть единственным образом расширены на всё C. Векторное пространство C становится коалгеброй с коумножением Δ и коединицей ε (проверка этого является хорошим способом получения используемых аксиом).

Конечномерный случай

В конечномерном случае, дуальность между алгеброй и коалгеброй ближе: дуальная конечномерная (унитарная ассоциативная) алгебра есть коалгебра, если дуальная конечномерная коалгебра есть (унитарная ассоциативная) алгебра. Вообще говоря, дуальная алгебра может не быть коалгеброй.

Примечания

1. ↑ Yokonuma (1992), Шаблон:Google books quote, Prop. 1.7.
2. ↑ Yokonuma (1992), Шаблон:Google books quote, Prop. 1.4.

См. также

• Комодуль
• Биалгебра
• Алгебра Хопфа

Ссылки

• Dăscălescu, Sorin; Năstăsescu, Constantin & Raianu, Șerban (2001), «Hopf Algebras», vol. 235 (1st ed.), Pure and Applied Mathematics, Marcel Dekker, ISBN 0-8247-0481-9 .
• Yokonuma, Takeo (1992), «Tensor spaces and exterior algebra», vol. 108, Translations of mathematical monographs, AMS Bookstore, ISBN 9780821845646 .
• Chapter III, section 11 in Bourbaki Nicolas Algebra. — Springer-Verlag, 1989. — ISBN 0-387-19373-1

Внешние ссылки

• William Chin: A brief introduction to coalgebra representation theory