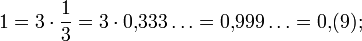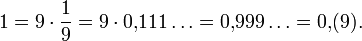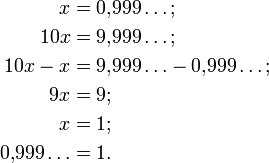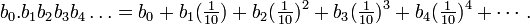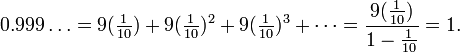- 0
-
0,(9)
0,(9) или 0,999… (
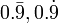 ) («ноль и девять в периоде») — периодическое десятичное число, которое в точности равно числу 1. То есть строки «0,999…» и «1» представляют одно и то же действительное число.
) («ноль и девять в периоде») — периодическое десятичное число, которое в точности равно числу 1. То есть строки «0,999…» и «1» представляют одно и то же действительное число.У этого равенства существует несколько доказательств разного уровня сложности, базирующихся как на свойствах действительных чисел, так и на дополнительных предположениях, исторических предпосылках и многом другом.
Содержание
Доказательства
Алгебраические
Деление столбиком
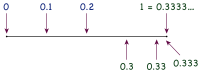
Часто рациональная дробь может быть представлена десятичной только с бесконечным хвостом. Используя деление столбиком, деление двух целых чисел, например 1⁄3 приводит к бесконечному 0.333… в десятичной записи, где цифры повторяются бесконечно. Таким образом легко доказывается равенство 0.999… = 1. Умножение 3 на 3 даёт 9 в каждом разряде, поэтому 3 × 0.333… эквивалентно 0.999…. И 3 × 1⁄3 эквивалентно 1, поэтому 0.999… = 1.[1]
Манипуляции с цифрами
Аналитические
Число 0.999… в общем виде можно записать как
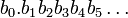
Бесконечные последовательности
В соответствии с определением позиционной системы счисления, посчитаем сумму ряда:
Для 0.999… применим теорему о сумме сходящейся геометрической прогрессии:[2]
- Если | r | < 1 , то
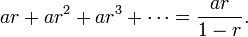
Радиус сходимости (знаменатель прогрессии)
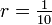 , и таким образом:
, и таким образом:Такое доказательство (в действительности что 10 эквивалентно 9.999…) было опубликовано в 1770 Леонардом Эйлером в издании Elements of Algebra.[3]
Формула суммы сходящейся геометрической прогрессии была известна до Эйлера. Выпущенный в 1811 учебник An Introduction to Algebra также использует геометрическую прогрессию для числа 0,(9) .[4] В 19 веке реакция на такое правило суммирования вылилась в утверждение: сумма ряда должна быть пределом последовательности частичных сумм. [5]
Последовательность (x0, x1, x2, …) имеет предел x тогда и только тогда, когда |x − xn| бесконечна мала с ростом n. Утверждение 0.999… = 1 может быть интерпретировано как предел:[6]
Последний шаг
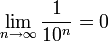 — делается на основании того, что действительные числа удовлетворяют аксиоме Архимеда.
— делается на основании того, что действительные числа удовлетворяют аксиоме Архимеда.Применение
Существует много применений, например в элементарной теории чисел. В 1802 H. Goodwin опубликовал наблюдение, обнаруженное им при делении на простые числа. Например:
- 1/7 = 0.142857142857… и 142 + 857 = 999.
- 1/73 = 0.0136986301369863… и 0136 + 9863 = 9999.
E. Midy в 1836 обобщил данные наблюдения в теорему: Midy's_theorem.
Примечания
- ↑ cf. with the binary version of the same argument in Silvanus P. Thompson, Calculus made easy, St. Martin's Press, New York, 1998. ISBN 0-312-18548-0.
- ↑ Rudin p.61, Theorem 3.26; J. Stewart p.706
- ↑ Euler p.170
- ↑ Grattan-Guinness p.69; Bonnycastle p.177
- ↑ For example, J. Stewart p.706, Rudin p.61, Protter and Morrey p.213, Pugh p.180, J.B. Conway p.31
- ↑ The limit follows, for example, from Rudin p. 57, Theorem 3.20e. For a more direct approach, see also Finney, Weir, Giordano (2001) Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Section 8.1, example 2(a), example 6(b).
См. также
Wikimedia Foundation. 2010.
-