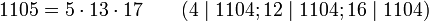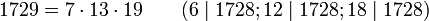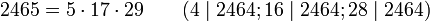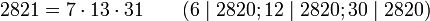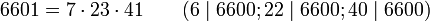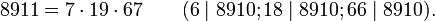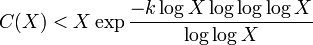Кармайкловы числа

Кармайкловы числа

В теории чисел кармайкловы числа — это положительные составные числа n, которые удовлетворяют условию 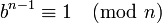$b^{n-1}\equiv 1\pmod{n}$ для всех целых b, взаимно простых с n (смотри Сравнение по модулю натурального числа).

Названы в честь Роберта Кармайкла.

Общее представление

Малая теорема Ферма утверждает, что любое простое число обладает выше указанным свойством. В этом смысле числа Кармайкла подобны простым. Поэтому они называются псевдопростыми числами.

Кроме того, с ростом чисел кармайкловы числа встречаются все реже. Например, между 1 и 10¹⁸ 1,401,644 чисел Кармайкла (примерно одно из миллиона миллионов).

Эквивалентное определение чисел Кармайкла дает критерий Корсельта.

Теорема (Корсельт, 1899): Составное число n является кармайкловым тогда и только тогда, когда n свободно от квадратов и для всех простых делителей p числа n верно p − 1 | n − 1 (обозначение a | b означает, что a делит b).

Из этой теоремы следует, что все числа Кармайкла нечётны, так как любое четное составное число, свободное от квадратов, имеет по крайней мере один нечетный простой делитель, и поэтому из p − 1 | n − 1 следует, что четное делит нечетное, что неверно — противоречие.

Корсельт был первым, что заметил эти свойства, но он так и не смог найти какие-либо примеры. В 1910 году Кармайкл нашел первое и наименьшее такое число, 561, откуда и название «Кармайкловы числа».

Следующие кармайкловы числа:

$1105 = 5 \cdot 13 \cdot 17 \qquad (4 \mid 1104; 12 \mid 1104; 16 \mid 1104)$

$1729 = 7 \cdot 13 \cdot 19 \qquad (6 \mid 1728; 12 \mid 1728; 18 \mid 1728)$

$2465 = 5 \cdot 17 \cdot 29 \qquad (4 \mid 2464; 16 \mid 2464; 28 \mid 2464)$

$2821 = 7 \cdot 13 \cdot 31 \qquad (6 \mid 2820; 12 \mid 2820; 30 \mid 2820)$

$6601 = 7 \cdot 23 \cdot 41 \qquad (6 \mid 6600; 22 \mid 6600; 40 \mid 6600)$

$8911 = 7 \cdot 19 \cdot 67 \qquad (6 \mid 8910; 18 \mid 8910; 66 \mid 8910).$

Cвойства

Кармайкловы числа имеют по меньшей мере три простых положительных множителя.

k
3	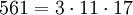$561 = 3 \cdot 11 \cdot 17$
4	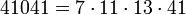$41041 = 7 \cdot 11 \cdot 13 \cdot 41$
5	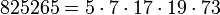$82526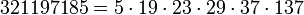5 = 5 \cdot 7 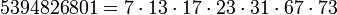\cdot 17 \cdot 19 \cdot 73$
6	$32119718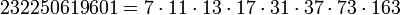5 = 5 \cdot 19 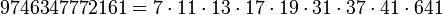\cdot 23 \cdot 29 \cdot 37 \cdot 137$
7	$5394826801 = 7 \cdot 13 \cdot 17 \cdot 23 \cdot 31 \cdot 67 \cdot 73$
8	$232250619601 = 7 \cdot 11 \cdot 13 \cdot 17 \cdot 31 \cdot 37 \cdot 73 \cdot 163$
9	$9746347772161 = 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 31 \cdot 37 \cdot 41 \cdot 641$

Первые кармайкловы числа с четырьмя простыми множителями:

i
1	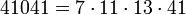$41041 = 7 \cdot 11 \cdot 13 \cdot 41$
2	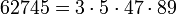$62745 = 3 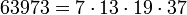\cdot 5 \cdot 4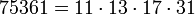7 \cdot 89$
3	$63973 = 7 \cdot 13 \cdot 19 \cdot 37$
4	$75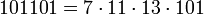36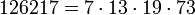1 = 11 \cdot 13 \cdot 17 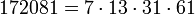\cdot 31$
5	$101101 = 7 \cdot 11 \cdot 13 \cdot 101$
6	$126217 = 7 \cdot 13 \cdot 19 \cdot 73$
7	$17208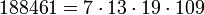1 = 7 \cdot 13 \cdot 31 \cdot 61$
8	$188461 = 7 \cdot 13 \cdot 19 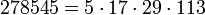\cdot 10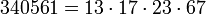9$
9	$278545 = 5 \cdot 17 \cdot 29 \cdot 113$
10	$340561 = 13 \cdot 17 \cdot 23 \cdot 67$

Распределение

Пусть C(X) обозначает количество чисел Кармайкла, меньших X. Эрдёш доказал в 1956 году, что

$C(X) < X \exp{\frac{-k \log{X} \log{\log{\log{X}}}}{\log{\log{X}}}}$

для некоторой константы k;

В следующей таблице приведены приближенные значения этой константы:

n	k
104	2.19547
106	1.97946
108	1.90495
1010	1.86870
1012	1.86377
1014	1.86293
1016	1.86406
1018	1.86522
1020	1.86598

Интересные факты

Второе кармайклово число (1105) может быть представлено как сумма двух квадратов большим количеством способов, чем любое меньшее число. Третье кармайклово число (1729) является числом Рамануджана — Харди (наименьшее число, представимое в виде суммы двух кубов двумя способами).