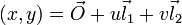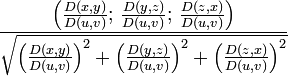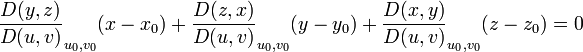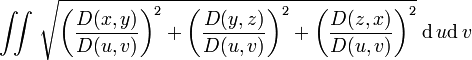Параметрическая поверхность

Класс трёхмерных параметрических поверхностей определяется функцией 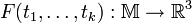$F(t_1,\ldots,t_k):\mathbb{M}\to\mathbb{R}^3$, зависящей от k параметров и отображающей некоторое связное множество 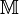$\mathbb{M}$ из n-мерного пространства в трёхмерное пространство таким образом, что это отображение является поверхностью. Эта функция F задаёт класс поверхностей, а набор k параметров - конкретную поверхность из этого класса.

Наиболее практичным является случай, когда множество 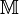$\mathbb{M}$ является единичным квадратом в двумерном пространстве. В этом случае параметрическую поверхность можно описать так:

(x,y,z) = F(u,v) или 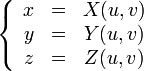$\left\{ \begin{array}{ccc} x &=& X(u,v) \\ y &=& Y(u,v) \\ z &=& Z(u,v) \end{array}\right.$, где $(u,v)\in[0,1]$

Параметрические поверхности широко используются в прикладной геометрии и компьютерной графике для представления сложных поверхностей. Параметризация делает такие поверхности удобными для обработки и отображения.

Параметризация простейших поверхностей

• Плоскость

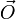Точка $\vec{O}$ и базис из двух неколлинеарных векторов 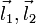$\vec{l}_1,\vec{l}_2$ в трёхмерном пространстве определяет плоскость и отображение на неё двумерной декартовой системы координат. Тем самым определяется uv-параметризация плоскости (u и v - параметры):

$(x,y)=\vec{O}+u\vec{l}_1+v\vec{l}_2$

• Плоский N-угольник

В общем случае параметризацию в N-угольнике можно ввести используя систему барицентрических координат.

• Треугольник

Этот важнейший частный случай N-угольника заслуживает особого внимания. Наиболее распространённый способ параметризации треугольника - линейное отображение на него треугольника из uv-пространства.

• Сфера

Для параметризации сферы удобнее всего использовать одноимённую систему координат:

$\left\{\begin{array}{ccc} x &=& \rho\sin\varphi\cos\theta \\ y &=& \rho\sin\varphi\sin\theta \\ z &=& \rho\cos\varphi\end{array}\right.,\quad \varphi\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right],\;\theta\in[0,2\pi)$.

• Цилиндр

Вполне естественно использовать цилиндрическую систему координат:

$\left\{\begin{array}{ccc} x &=& \rho\cos\varphi \\ y &=& \rho\sin\varphi \\ z &=& h\end{array}\right.,\quad \varphi\in[0,2\pi)$.

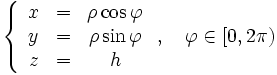Кривые поверхности

• Билинейный интерполяционный четырёхугольник

Упорядоченный набор из 4-х точек в пространстве 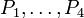$P_1,\ldots,P_4$ определяет билинейную интерполяционную поверхность и задаёт отображение на неё квадрата $u,v\in[0,1]$:

(x,y) = P₁uv + P₂(1 − u)v + P₃u(1 − v) + P₄(1 − u)(1 − v)

Эта поверхность является гладкой, однако невозможность задавать произвольные касательные на её границе делает её практически неприменимой в качестве патчей

• Поверхность Безье

На практике применяется в основном два вида поверхностей Безье: бикубическая 3-го порядка - четырёхугольник, определяемый 16-ю точками, и барицентрическая 3-го порядка - треугольник, определяемый 10 точками. Барицентрическая система координат в треугольнике содержит 3 числа, поэтому она не всегда удобна.

Граница поверхности Безье состоит из кривых Безье. Точки, определяющие поверхность, определяют также кривые её границы, включая нормали на них. Это позволяет создавать гладкие составные поверхности, то есть использовать поверхности Безье в качестве патчей

Рациональная поверхность Безье отличается тем, что каждой точке в её определении назначен некоторый «вес», определяющий степень её влияния на форму поверхности.

• B-сплайновая поверхность

На практике обычно применяются бикубические B-сплайновые поверхности. Как и поверхности Безье, они определяются 16-ю точками, однако в общем случае не проходят через эти точки. Однако B-сплайны удобно использовать в качестве патчей, так как они хорошо стыкуются друг с другом при использовании общей сетки вершин, а сами вершины позволяют явным образом задавать нормали и касательные на границах патчей.

При необходимости более гибкого управления формой поверхности применяют рациональные B-сплайны, неоднородные B-сплайны, а также комбинированный вариант - неоднородные рациональные B-сплайны (NURBS).

Свойства параметрических поверхностей

Пусть 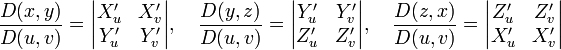$\frac{D(x,y)}{D(u,v)}=\begin{vmatrix}X'_u & X'_v \\ Y'_u & Y'_v \end{vmatrix},\quad\frac{D(y,z)}{D(u,v)}=\begin{vmatrix}Y'_u & Y'_v \\ Z'_u & Z'_v \end{vmatrix},\quad\frac{D(z,x)}{D(u,v)}=\begin{vmatrix}Z'_u & Z'_v \\ X'_u & X'_v \end{vmatrix}$. Тогда:

• Нормаль в точке поверхности определяется выражением:
  

$\frac{\left(\frac{D(x,y)}{D(u,v)};\,\frac{D(y,z)}{D(u,v)};\,\frac{D(z,x)}{D(u,v)}\right)}{\sqrt{\left(\frac{D(x,y)}{D(u,v)}\right)^2+\left(\frac{D(y,z)}{D(u,v)}\right)^2+\left(\frac{D(z,x)}{D(u,v)}\right)^2}}$

• Касательная плоскость в заданной точке может быть описана уравнением:
  

$\frac{D(y,z)}{D(u,v)}_{u_0,v_0}(x-x_0)+\frac{D(z,x)}{D(u,v)}_{u_0,v_0}(y-y_0)+\frac{D(x,y)}{D(u,v)}_{u_0,v_0}(z-z_0)=0$

• Площадь параметрически заданной поверхности рассчитывается по формулам:
  

$\iint\,\sqrt{\left(\frac{D(x,y)}{D(u,v)}\right)^2+\left(\frac{D(y,z)}{D(u,v)}\right)^2+\left(\frac{D(z,x)}{D(u,v)}\right)^2}\;\mathrm{d}\,u\mathrm{d}\,v$

Или

$\iint\,\left|[\dot{r}_u\times\dot{r}_v]\right|\;\mathrm{d}\,u\;\mathrm{d}\,v$, где $\dot{r}_u=\left(\frac{\partial x}{\partial u},\,\frac{\partial y}{\partial u},\,\frac{\partial z}{\partial u}\right), \quad \dot{r}_v=\left(\frac{\partial x}{\partial v},\,\frac{\partial y}{\partial v},\,\frac{\partial z}{\partial v}\right)$

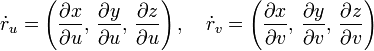
Литература

• Ильин В.А., Позняк Э.Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
• Кудрявцев Л.Д. Курс математического анализа. — М.: Дрофа. — 570 с.
• Роджерс Д.,Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001. — ISBN 5-03-002143-4