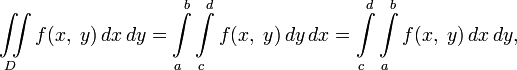- Теорема Тонелли — Фубини
-
Теорема Тонелли — Фубини
Теоре́ма Тоне́лли — Фуби́ни в математическом анализе, теории вероятностей и смежных дисциплинах сводит вычисление двойного интеграла к повторным.
Содержание
Формулировка
Пусть даны два пространства с σ-конечными мерами
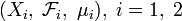 . Обозначим через
. Обозначим через 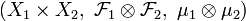 их произведение. Пусть функция
их произведение. Пусть функция 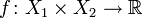 интегрируема относительно меры
интегрируема относительно меры 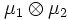 . Тогда
. Тогда- функция
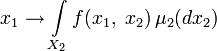 определена и интегрируема относительно μ1;
определена и интегрируема относительно μ1; - функция
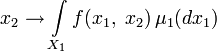 определена и интегрируема относительно μ2;
определена и интегрируема относительно μ2; - имеют место равенства
и
Частные случаи
Теория вероятностей
Пусть
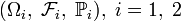 — вероятностные пространства, и
— вероятностные пространства, и 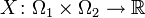 — случайная величина на
— случайная величина на 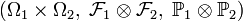 . Тогда
. Тогдагде индекс обозначает вероятностную меру, относительно которой берётся математическое ожидание.
Математический анализ
Пусть
![f\colon D=[a,\;b]\times[c,\;d]\to\R](http://dic.academic.ru/pictures/wiki/files/50/256ba9da6668c4db89f2959f35aa395d.png) функция двух переменных, интегрируемая по Риману на прямоугольнике
функция двух переменных, интегрируемая по Риману на прямоугольнике ![[a,\;b]\times[c,\;d]](http://dic.academic.ru/pictures/wiki/files/56/8a2c54ae7602ffb68153792d1dd06c40.png) , то есть
, то есть 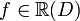 . Тогда
. Тогдагде интеграл в левой части двумерный, а остальные повторные одномерные.
Доказательство
Любое разбиение λ множества
![[a,\;b]\times[c,\;d]](http://dic.academic.ru/pictures/wiki/files/56/8a2c54ae7602ffb68153792d1dd06c40.png) получено некоторыми разбиениями λx отрезка
получено некоторыми разбиениями λx отрезка ![X=[a,\;b]](http://dic.academic.ru/pictures/wiki/files/57/91dae3ca5d9c917f667e4718429e9082.png) и λy отрезка
и λy отрезка ![[c,\;d]](http://dic.academic.ru/pictures/wiki/files/99/c6cc3508bf591e0a4468f6489bfbbd1a.png) , при этом объём любого прямоугольника
, при этом объём любого прямоугольника 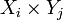 определяется
определяется 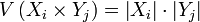 , где Xi,Yj ― некоторые частичные отрезки разбиений. Тогда рассмотрим следующие оценки интеграла
, где Xi,Yj ― некоторые частичные отрезки разбиений. Тогда рассмотрим следующие оценки интеграла 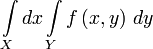 и нижних и верхних интегральных сумм функции
и нижних и верхних интегральных сумм функции 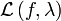 и
и 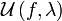 :
:
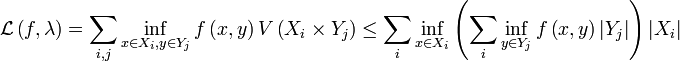
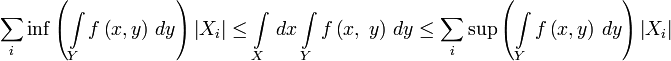
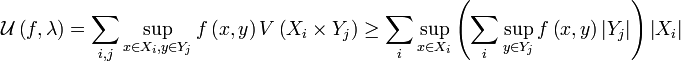
Тогда при интегрируемости f по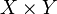 , то есть равенстве
, то есть равенстве 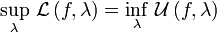 из вышеуказанных оценок интеграл
из вышеуказанных оценок интеграл 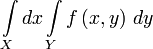 также существует и имеет такое же значение, как и
также существует и имеет такое же значение, как и 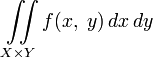
См. также
Литература
- Зорич В.А. Математический анализ. — М.: Наука Главная редакция физико-математической литературы, 1984. — С. 131-138.
Wikimedia Foundation. 2010.
- функция
Теорема Тонелли — Теорема Тонелли Фубини в математическом анализе, теории вероятностей и смежных дисциплинах сводит вычисление двойного интеграла к повторным. Содержание 1 Формулировка 2 Частные случаи … Википедия
Анализ функций многих переменных — Эта статья или раздел грубый перевод статьи на другом языке (см. Проверка переводов). Он мог быть сгенерирован программой переводчиком или сделан человеком со слабыми познаниями в языке оригинала. Вы можете помочь … Википедия
Интеграл Даниэля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниэлем (Daniell) в 1918 году в его… … Википедия
Кратный интеграл — В математическом анализе кратным или многократным интегралом называют множество интегралов, взятых от переменных. Например: Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число. Содержание 1… … Википедия
Интеграл Даниеля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниелем (англ.) в 1918 году в его… … Википедия
Независимость (теория вероятностей) — У этого термина существуют и другие значения, см. Независимость (значения). В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные … Википедия
Произведение мер — в функциональном анализе, теории вероятностей и смежных дисциплинах формальный способ построить меру на декартовом произведении двух пространств с мерами. Содержание 1 Построение 2 Замечания 3 Пример … Википедия
Многомерное исчисление — (также известное как многовариантное исчисление) является расширением исчисления функций одной переменной в исчисление функций нескольких переменных: функции, которые дифференцируются и интегрируются, затрагивая несколько переменных, а не одну.… … Википедия

![\iint\limits_{X_1\times X_2}f(x_1,\;x_2)\,\mu_1\otimes\mu_2(dx_1\,dx_2)=\int\limits_{X_1}\left[\;\,\int\limits_{X_2}f(x_1,\;x_2)\,\mu_2(dx_2)\right]\,\mu_1(dx_1)](http://dic.academic.ru/pictures/wiki/files/101/e5a6a0b2042eb4ea19db31d4d88bf1fe.png)
![\iint\limits_{X_1\times X_2}f(x_1,\;x_2)\,\mu_1\otimes\mu_2(dx_1\,dx_2)=\int\limits_{X_2}\left[\;\,\int\limits_{X_1}f(x_1,\;x_2)\,\mu_1(dx_1)\right]\,\mu_2(dx_2).](http://dic.academic.ru/pictures/wiki/files/102/f5a44094def8c59c253111465bdc23ae.png)
![\mathbb{E}_{\mathbb{P}_1\otimes\mathbb{P}_2}[X]=\mathbb{E}_{\mathbb{P}_1}\left[\mathbb{E}_{\mathbb{P}_2}[X]\right]=\mathbb{E}_{\mathbb{P}_2}\left[\mathbb{E}_{\mathbb{P}_1}[X]\right],](http://dic.academic.ru/pictures/wiki/files/51/30fab4604f16ed07457c0b4420d1b6a9.png)