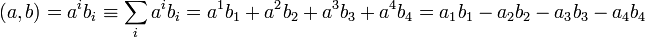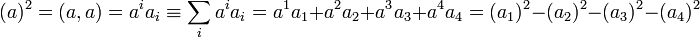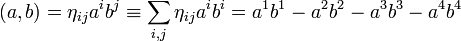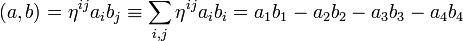Четырёхвектор

4-вектором (четырёхвектором, четыре-вектором) называется вектор в четырёхмерном пространстве Минковского. Координаты 4-вектора при переносе или повороте системы отсчёта преобразуются как соответствующие им координаты в пространстве Минковского. В 4-векторе одна временная компонента и три пространственных. Пространственные компоненты составляют обычный пространственный трёхмерный вектор и преобразуются в соответствии с этим при преобразовании пространственных координат, не затрагивающих временной, то есть при преобразованиях координат, не включающих физического движения новой системы системы отсчёта относительно прежней.

• В современных обозначениях временной компоненте обычно соответствует индекс 0 (то есть она считается нулевой компонентой), пространственным: 1,2,3 — совпадающим с x, y, z (обычно, по умолчанию и если возможно, это обычные прямоугольные декартовы координаты). В старой литературе часто используется соглашение (восходящее к Минковскому), по которому временная компонента считалась не нулевой, а четвёртой.
• Иногда бывает удобно приписывать временной компоненте 4-вектора чисто мнимый характер (всегда умножать действительную временную компоненту на мнимую единицу). Такое представление 4-векторов было исторически введено первым, однако не слишком редко — в силу своего удобства — используется и в современной литературе.
• 4-векторы (их компонентное представление) могут быть записаны в контравариантной и (или) ковариантной форме (см. ниже), которые не всегда совпадают, а в случае действительного представления (без мнимой единицы) всегда различаются между собой, хотя в простых случаях это различие весьма просто.

4-векторами являются

• 4-перемещение $~dx^i = ( c ~dt, dx, dy, dz )$,

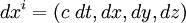• 4-скорость 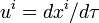$~u^i = dx^i / d\tau$, где τ — «собственное время», равное интервалу, измеренному вдоль мировой линии,

• 4-ускорение 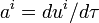$~a^i = du^i / d\tau$, где τ — см. выше,

• 4-вектор энергии-импульса (4-импульс),

• четырёхмерная плотность тока $~j^i = (c \rho,j_x,j_y,j_z)$,

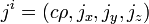• волновой 4-вектор $~k_i = ( \frac{1}{c}\omega, -k_x, -k_y, -k_z )$,

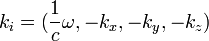• электромагнитный потенциал $~A_i = ( \phi, -A_x, -A_y, -A_z )$,

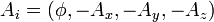и т. д.

Закон преобразование четырёхвектора:

$~ \tilde A^i=\sum_i S_j^i\ A^j$,

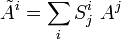где 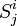$S_j^i$ — матрица из группы Лоренца — матрица перехода к новым координатам (к новой системе отсчёта).

• Скалярные произведения (в частности, квадраты) 4-векторов вычисляются с использованием метрики Лоренца (см. также ниже).

• • Они инвариантны относительно преобразований Лоренца. Они называются скалярами (в четырёхмерном — пространственно-временном — смысле).

• • Например, это интервал (квадрат интервала есть квадрат вектора перемещения в метрике Лоренца), масса (масса покоя) — её квадрат есть, с точностью до постоянного множителя, квадрат 4-импульса: m² = E² / c⁴ − p² / c² и т. д.

Обозначения

Традиционно используется обозначение 4-вектора как совокупности его компонент. Так 4-вектор a обозначается как: aⁱ (не нужно путать это обозначение с возведением в степень!) или a_i.

Координаты, пространственную и временную, обычно обозначают как xⁱ.

Что означает при этом использование верхнего (aⁱ) или нижнего a_i индекса, оговаривается особо, но по умолчанию, если используется тот и другой (или хотя бы первый) вариант, то есть, если верхние индексы вообще используют, верхним индексом обозначают контравариантные координаты 4-вектора, а нижним — ковариантные координаты. Таким образом, в этом случае один и тот же вектор может иметь два разных представления — контравариантное (быть представлен как контравариантный вектор) и ковариантное (быть представлен как ковариантный вектор).

В случае плоского пространства и инерциальных систем отсчета, как в электродинамике, специальной теории относительности и вообще в случаях, когда гравитацией можно пренебречь, ковариантное и контравариантное представление отличаются лишь знаком временной (или наоборот, в зависимости от условно принятой сигнатуры — пространственных) компоненты. При этом скалярное произведение представимо как простая сумма произведений соответствующих компонент только для произведения ковариантного вектора с контравариантным, например:

$(a,b) = a^i b_i \equiv \sum_i a^i b_i = a^1 b_1 + a^2 b_2 + a^3 b_3 + a^4 b_4 = a_1 b_1 - a_2 b_2 - a_3 b_3 - a_4 b_4$

и в частности

$(a)^2 = (a,a) = a^i a_i \equiv \sum_i a^i a_i = a^1 a_1 + a^2 a_2 + a^3 a_3 + a^4 a_4 = (a_1)^2 - (a_2)^2 - (a_3)^2 - (a_4)^2$

(здесь и ниже использовано правило суммирования по повторяющемуся индексу Эйнштейна, а возведение в квадрат обозначено как (…)²).

Если же хотят написать скалярное произведение с использованием только ковариантных или только контравариантных компонент, обычно используют запись с метрикой Лоренца η_ij (или η^ij):

$(a,b) = \eta_{ij} a^i b^j \equiv \sum_{i,j} \eta_{ij} a^i b^i = a^1 b^1 - a^2 b^2 - a^3 b^3 - a^4 b^4$

или

$(a,b) = \eta^{ij} a_i b_j \equiv \sum_{i,j} \eta^{ij} a_i b_i = a_1 b_1 - a_2 b_2 - a_3 b_3 - a_4 b_4$

(оба способа эквивалентны друг другу и описанному выше способу со обоими типами координат).

Однако в более общем случае нелоренцевых систем отсчета, в том числе при учете гравитации в соответствии с ОТО, вместо очень простой и постоянной лоренцевой метрики η_ij приходится рассматривать произвольную, в том числе зависящую от пространственных координат и времени метрику g_ij. (Во всех формулах, написанных в этом параграфе выше надо в общем случае заменить η_ij на g_ij, а η^ij на g^ij). При этом простое правило о том, что ковариантное и контравариантное представление 4-вектора различаются лишь знаком пространственных компонент, перестает действовать, они начинают выражаться друг через друга с использованием также метрики g_ij общего вида (см. Метрический тензор#Изоморфизм между касательным и кокасательным пространством):

$a^i = g^{ij} a_j \equiv \sum_j g^{ij} a_j$,

$a_i = g_{ij} a^j \equiv \sum_j g_{ij} a^j$.

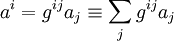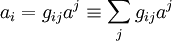(Как видим, эти формулы были верны и для η_ij, но в том случае сводились к простому правилу перемены знака некоторых компонент, а здесь — в общем случае — уже не сводятся).

Заметим также, что в пространстве-времени с кривизной (которое уже правильно считать только многообразием, а не векторным пространством), совокупность координат xⁱ уже не является вектором. Однако, бесконечно малые смещения по координатам dxⁱ представляют вектор (вектор касательного пространства к многообразию в точке xⁱ).

И наконец, в случае лоренцевой метрики, рассмотренном выше, нередко используют только нижние индексы, так как ковариантные и контравариантные компоненты различаются только знаком, и можно ограничиваться упоминанием только одних из них (обычно — контравариантных, хотя и используя нижний индекс). Этот способ для этого случая сравнительно удобен, так как отсутствие верхних индексов несколько более привычно для неспециалистов, к тому же не может создать путаницы с обозначением возведения в степень. Однако и он имеет подводные камни, так как, например, вектор 4-градиента, записанный в контравариантном виде, довольно неожиданно имеет знак минус у пространственных компонент: 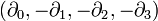$(\partial_0, -\partial_1, -\partial_2, -\partial_3)$, так как полный дифференциал 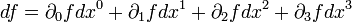$df = \partial_0 f dx^0 + \partial_1 f dx^1 + \partial_2 f dx^2 + \partial_3 f dx^3$ — должен быть инвариантным, а в формулу скалярного произведения, если оба вектора представлены в одинаковой контравариантной форме, входит, как мы знаем, изменение знака из-за ηij.

Интересно, что способ с использованием только нижних индексов и мнимой временной компоненты лишен этих недостатков (главным образом в области применимости, ограниченной случаем плоского пространства, но не только). Дело в том, что при использовании этого способа нужные знаки получаются автоматически (внимание: с учетом сигнатуры; впрочем, выбор сигнатуры — всё равно дело договоренности). То есть, о знаках вообще не нужно думать, не нужно использовать явно матрицу метрического тензора, даже ηij, то есть метрика формально представлена единичной матрицей («формально евклидовская», что, конечно, не меняет её реально псевдоевклидова характера, но упрощает запись), а представление всех 4-векторов просто и единообразно:

• 4-перемещение $~dx_\mu = ( i c ~dt, dx, dy, dz )$,
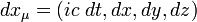• 4-импульс $~p_\mu = ( i E / c, p_x, p_y, p_z )$,
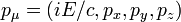• четырёхмерная плотность тока $~j_\mu = ( i c \rho,j_x,j_y,j_z)$,
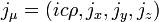• волновой 4-вектор $~k_\mu = ( i \omega / c, k_x, k_y, k_z )$,
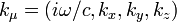• электромагнитный потенциал $~A_\mu = ( i \phi, A_x, A_y, A_z )$,

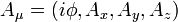и т. д., где i - мнимая единица.

4-вектор в математике

Точка в пространстве Минковского называется событием и задаётся четырьмя координатами:

$\mathbf{x} := \left(ct, x, y, z \right)$,

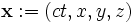где c — скорость света, t — время события, а x,y,z — его пространственные координаты. Такой 4-вектор называется 4-радиус-вектором.

Многие другие 4-векторы могут быть построены из него и далее друг из друга сложением, вычитанием, умножением или делением на скаляр, а также дифференцированием по скаляру и т. п. Так из 4-радиусвектора дифференцированием по собственному времени получается 4-скорость, и т. д.

Скалярные произведения 4-векторов — лоренц-инвариантные величины (инварианты группы Лоренца), скаляры пространства Минковского.

История

4-векторы впервые рассмотрели Пуанкаре (1905) и затем Минковский. Они рассматривали временную компоненту 4-вектора чисто мнимой, что автоматически порождало нужное правило вычисления скалярного произведения при обычном суммировании произведений компонент.

Литература

• Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7, §6. Четырёхмерные векторы.
• Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 6: Электродинамика. Перевод с английского (издание 3). — Эдиториал УРСС. — ISBN 5-354-00704-6 - гл.25. "Электродинамика в релятивистских обозначениях". (Это простое введение для студентов младших курсов; во избежание путаницы следует обратить внимание, что в этой книге используются только нижние индексы, относящиеся однако к контравариантным компонентам 4-векторов).