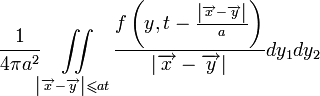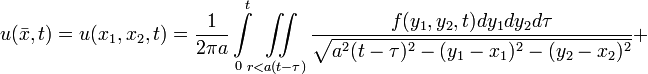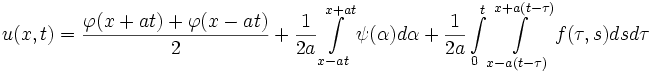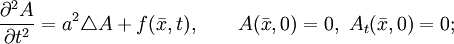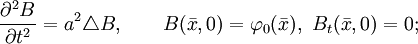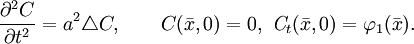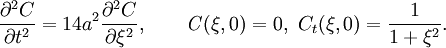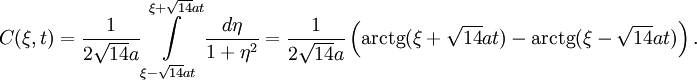- Формула Пуассона
-
Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.
Содержание
Полная формулировка задачи и ответа
Рассмотрим уравнение
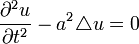 , где функция
, где функция 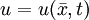 определена на
определена на 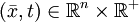 .
.
Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a в моменты времени t > 0.
Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t = 0:
Тогда обобщённая формула Кирхгофа даёт решение этой задачи.
Сам Кирхгоф рассматривал только трёхмерный случай.
Идея получения решения
Простой вывод решения основной задачи использует преобразование Фурье. Обобщенная формула Кирхгофа имеет следующий вид:
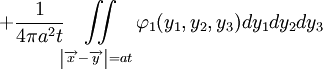 .
.В случае, если в волновом уравнении имеется правая часть f, в правой части формулы появится слагаемое:
Физические следствия
 Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени
Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времениПусть в начальный момент времени t = 0 на некотором компакте M есть локальное возмущение (
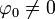 и/или
и/или 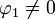 ). Если мы находимся в некоторой точке
). Если мы находимся в некоторой точке 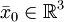 , то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время
, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время  .
.Вне отрезка времени
![\left [ t_1; t_2 \right ]](/pictures/wiki/files/53/5d5ba987b60dc461bdd45f684fbbb972.png) , где
, где 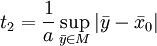 , функция u(x 0, t) равна нулю.
, функция u(x 0, t) равна нулю.Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в
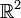 , уже не будет компактным в
, уже не будет компактным в 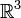 , а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).
, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).Формула Пуассона-Парсеваля
Решение уравнения колебаний мембраны
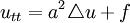
- (функция f(x,t) соответствует вынуждающей внешней силе)
с начальными условиями
задаётся формулой:
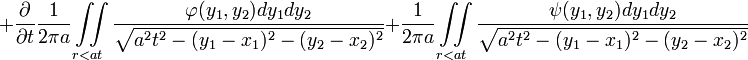 .
.Формула Д'Аламбера
Решение одномерного волнового уравнения
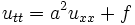 (функция f(x,t) соответствует вынуждающей внешней силе)
(функция f(x,t) соответствует вынуждающей внешней силе)
с начальными условиями
имеет вид
 В область II приходят характеристики только из одного семейства
В область II приходят характеристики только из одного семействаПри пользовании формулой Д'Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области
![\mathbb{R}^1\times[0, T]](/pictures/wiki/files/54/646dccb00d2a6f780af669cc41c1f840.png) . Решение волнового уравнения представляется в виде суммы двух функций: u(x,t) = f(x + at) + g(x − at), то есть оно определяется двумя семействами характеристик:
. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t) = f(x + at) + g(x − at), то есть оно определяется двумя семействами характеристик: 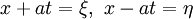 . Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д'Аламбера не работает.
. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д'Аламбера не работает.Применение формул
В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения
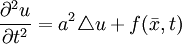 с начальными условиями
с начальными условиями 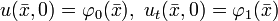 и искать решение в виде суммы трех функций: u(x,t) = A(x,t) + B(x,t) + C(x,t), которые удовлетворяют следующим условиям:
и искать решение в виде суммы трех функций: u(x,t) = A(x,t) + B(x,t) + C(x,t), которые удовлетворяют следующим условиям:Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путем замены переменных. Например, пусть
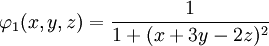 . Тогда, сделав замену ξ = x + 3y − 2z, уравнение для задачи "С" примет вид:
. Тогда, сделав замену ξ = x + 3y − 2z, уравнение для задачи "С" примет вид:Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д'Аламбера:
В силу четности начального условия, решение сохранит свой вид во всей области t > 0.
Литература
Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6
Ссылки
Wikimedia Foundation. 2010.

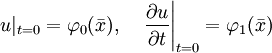
![u(\overrightarrow{x},t)=u(x_1,x_2,x_3,t)=
\frac{\partial}{\partial t}\left [ \frac{1}{4\pi a^2t}\iint\limits_{\left | \overrightarrow{x}-\overrightarrow{y}\right | =at}\varphi_0(y_1,y_2,y_3)dy_1 dy_2 dy_3 \right ] +](/pictures/wiki/files/49/192191ff6c5a81ddfafb352435a6dd3e.png)