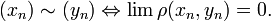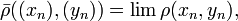- Условие Коши
-
Последовательность точек
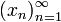 метрического пространства с метрикой ρ называется фундаментальной (ρ-фундаментальной) или последовательностью Коши, если она удовлетворяет критерию Коши:
метрического пространства с метрикой ρ называется фундаментальной (ρ-фундаментальной) или последовательностью Коши, если она удовлетворяет критерию Коши:Для любого
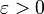 существует такое натуральное
существует такое натуральное 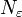 , что
, что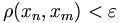 для всех
для всех 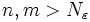 .
.
Любая сходящаяся последовательность фундаментальна. Пусть a — её предел. Тогда, начиная с некоторого N,
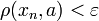 и
и 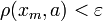 , а стало быть,
, а стало быть, 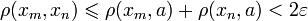 , значит, последовательность по определению фундаментальна.
, значит, последовательность по определению фундаментальна.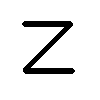
Обратное, в общем случае, неверно. Во множестве рациональных чисел
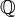 , рассматриваемом как метрическое пространство с метрикой, определяемой обычной абсолютной величиной ρ(x,y) = | x − y | последовательность десятичных дробей, приближающих какое-нибудь иррациональное число, например π с недостатком — 3; 3,1; 3,14; 3,141… является фундаментальной, но во множестве рациональных чисел не имеет предела, так как π иррационально.
, рассматриваемом как метрическое пространство с метрикой, определяемой обычной абсолютной величиной ρ(x,y) = | x − y | последовательность десятичных дробей, приближающих какое-нибудь иррациональное число, например π с недостатком — 3; 3,1; 3,14; 3,141… является фундаментальной, но во множестве рациональных чисел не имеет предела, так как π иррационально.Содержание
Полное пространство
Метрическое пространство называется полным, если любая фундаментальная последовательность в нём сходится.
Полнота множества действительных чисел
Как уже было показано, множество рациональных чисел
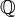 с обычной метрикой неполно. Покажем, что множество действительных чисел
с обычной метрикой неполно. Покажем, что множество действительных чисел 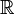 образует полное пространство, то есть любая фундаментальная последовательность действительных чисел является сходящейся. Пусть некая последовательность (xn) удовлетворяет критерию Коши. Тогда она, очевидно, ограничена. Следовательно, по теореме Больцано — Вейерштрасса у неё существует предельная точка. Чтобы доказать существование (конечного) предела, необходимо доказать единственность предельной точки. Пусть их существует две — a1 и a2. Тогда возьмём
образует полное пространство, то есть любая фундаментальная последовательность действительных чисел является сходящейся. Пусть некая последовательность (xn) удовлетворяет критерию Коши. Тогда она, очевидно, ограничена. Следовательно, по теореме Больцано — Вейерштрасса у неё существует предельная точка. Чтобы доказать существование (конечного) предела, необходимо доказать единственность предельной точки. Пусть их существует две — a1 и a2. Тогда возьмём 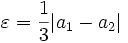 . Так как a1 и a2 — предельные точки последовательности, то для любого номера N, в том числе соответствующего в определении фундаментальной последовательности для данного
. Так как a1 и a2 — предельные точки последовательности, то для любого номера N, в том числе соответствующего в определении фундаментальной последовательности для данного  , будут существовать n и m, большие N и такие, что xn и xm будут находиться в ε-окрестностях предельных точек a1 и a2 соответственно, а значит, расстояние между точками a1 и a2 будет
, будут существовать n и m, большие N и такие, что xn и xm будут находиться в ε-окрестностях предельных точек a1 и a2 соответственно, а значит, расстояние между точками a1 и a2 будет 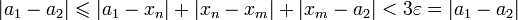 , что противоречит условию. То что любая сходящаяся последовательность фундаментальна было показано выше. Таким образом для последовательностей действительных чисел фундаментальность является необходимым и достаточным условием сходимости (условие Коши).
, что противоречит условию. То что любая сходящаяся последовательность фундаментальна было показано выше. Таким образом для последовательностей действительных чисел фундаментальность является необходимым и достаточным условием сходимости (условие Коши).Другие примеры полных пространств
- любое конечномерное евклидово или эрмитово пространство полно.
- любое банахово пространство, в частности гильбертово пространство, полно по определению.
Пополнение
Всякое метрическое пространство X = (X,ρ) можно вложить в полное пространство Y таким образом, что метрика Y продолжает метрику X, а подпространство X всюду плотно в Y. Такое пространство Y называется пополнением и обычно обозначается
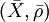 . Любые два пополнения изометричны. Один из самых простых способов построения пополнения следующий. Для любого метрического пространства X = (X,ρ), на множестве фундаментальных последовательностей в X можно ввести отношение эквивалентности
. Любые два пополнения изометричны. Один из самых простых способов построения пополнения следующий. Для любого метрического пространства X = (X,ρ), на множестве фундаментальных последовательностей в X можно ввести отношение эквивалентностиМножество классов эквивалентности
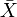 с метрикой, определённой
с метрикой, определённойявляется метрическим пространством. Само пространство (X,ρ) изометрически вкладывается в него следующим образом: точке
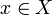 соответствует класс постоянной последовательность xn = x. Получившееся пространство
соответствует класс постоянной последовательность xn = x. Получившееся пространство 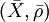 и будет пополнением X. Если X имеет алгебраическую структуру, например кольца, то она естественным образом переносится на
и будет пополнением X. Если X имеет алгебраическую структуру, например кольца, то она естественным образом переносится на 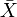 .
.Примеры пополнений
- Поле действительных чисел
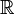 является пополнением поля рациональных чисел
является пополнением поля рациональных чисел 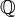 при помощи метрики, определяемой обычной абсолютной величиной.
при помощи метрики, определяемой обычной абсолютной величиной. - Поле p-адических чисел
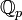 является пополнением при помощи метрики, определяемой p-адическим нормированием.
является пополнением при помощи метрики, определяемой p-адическим нормированием.
Литература
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, — М.: Наука, 2004. — 7-е изд.
- Шилов Г. Е. Математический анализ. Функции одного переменного. Ч.3, — М.:Наука, 1970.
Wikimedia Foundation. 2010.