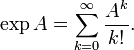Матричная экспонента

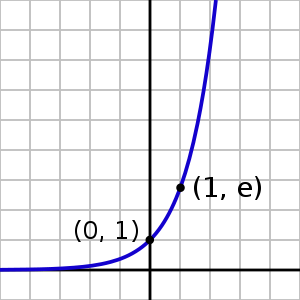
Экспонента — функция exp(x) = e^x, где e — основание натуральных логарифмов.

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

$e^x=\sum_{k=0}^\infty \frac{x^k}{k!}$

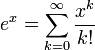
или через предел:

$e^x=\lim_{n\rightarrow \infty} (1+\frac{x}{n})^n$

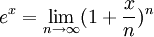
Здесь x — любое вещественное или комплексное число.

Свойства

• (e^x)' = e^x, в частности
• Экспонента является единственным решением дифференциального уравнения y' = y с начальными данными y(0) = 1. Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
• Экспонента является выпуклой функцией.
• Обратная функция к ней — натуральный логарифм $\ln~a$.
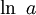• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
• Основное функциональное свойство экспоненты:

  exp(a + b) = exp(a)exp(b).

  • Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид exp(ct), где c — некоторая константа.

Экспонента от комплексного аргумента

От комплексного аргумента z = x + iy экспонента определяется следующим образом:

e^z = e^{x + iy} = e^xe^iy = e^x(cosy + isiny) (формула Эйлера)

В частности,

e^iπ + 1 = 0

Вариации и обобщения

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

$\exp A=\sum_{k=0}^{\infty} \frac{A^k}{k!}.$

Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: 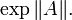$\exp \|A\|.$ Следовательно, экспонента от матрицы 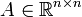$A \in \Bbb{R}^{n\times n}$ всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 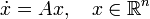$\dot x=Ax, ~~~ x\in \mathbb R^n$ с начальным условием x(0) = x₀ имеет своим решением x(t) = exp(At)x₀.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x):

ln(x) = log_e(x)

См. также

• Экспонента комплексного переменного (обобщение)
• Показательная функция