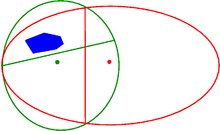
Метод эллипсоидов

Метод эллипсоидов — алгоритм нахождения точки, лежащей в пересечении выпуклых множеств.

Описание алгоритма

В начале выбирается большой шар, содержащий пересечение выпуклых множеств. Способ построения этого шара зависит от задачи. Далее на каждом шаге имеется эллипсоид, заданный центром $v$ и векторами $v_1, v_2, \dots, v_n \in \mathbb{R}^n$. Эллипсоиду принадлежат точки $v+c_1v_1+c_2v_2+\cdots+c_nv_n$ для которых $c_1^2+c_2^2+\cdots+c_n^2\le 1$. Отметим, что один и тот же эллипсоид можно задать несколькими способами. Если центр этого эллипсоида принадлежит всем выпуклым множествам, то искомая точка найдена. Иначе существует гиперплоскость $\pi$, проходящая через точку $v$, такая, что одно из множеств целиком лежит по одну сторону от нее. Тогда можно перейти от исходного базиса $v_i$ к другому базису $\tau, w_2, \dots w_n$ такому, что $w_i$ параллельны $\pi$, а $\tau$ направлен в сторону множества. Положим теперь $v'=v+\frac{\tau}{n+1}$, $v'_1=\frac{n\tau}{n+1}$, $v'_i=w_i\frac{n}{\sqrt{n^2-1}}$ при $i\ge 2$. Этот новый эллипсоид содержит половину старого и имеет меньший объем. Таким образом, объем эллипсоида уменьшается экспоненциально с ростом числа шагов и искомая точка будет найдена за $O(n^2\log(V_1/V_2))$ шагов, где $V_1$ — объем исходного шара, а $V_2$ — объем области пересечения. Общее время работы алгоритма получается равным $O(Ntn^2\log(V_1/V_2))$, где $N$ — число множеств, $t$ — время проверки принадлежности точки множеству.

Применение к задаче линейного программирования

Если в задаче линейного программирования удалось построить шар, содержащий искомое решение, то она может быть решена методом эллипсоидов. Для этого вначале находим какую-нибудь точку $u$ внутри шара, удовлетворяющую ограничениям задачи. Проводим через нее гиперплоскость $f(x)<f(u)$, где $f$ — целевая функция, и находим точку в пересечении исходных и новой гиперплоскостей (начиная с текущего эллипсоида). С новой найденной точкой проделываем то же самое. Процесс сходится к оптимальному решению с экспоненциальной скоростью (поскольку с этой скоростью убывает объем эллипсоида).