- Случайное блуждание
-
Теория случайных блужданий — теория, согласно которой изменения стоимости ценных бумаг колеблются случайным образом вокруг своей объективной цены, оппонирует теории технического анализа.
Содержание
Одномерное дискретное случайное блуждание
Одномерное дискретное случайное блуждание — это случайный процесс
 с дискретным временем, имеющий вид
с дискретным временем, имеющий вид ,
,
где
 — начальное состояние;
— начальное состояние; ;
;- случайные величины
 совместно независимы.
совместно независимы.
Случайное блуждание как цепь Маркова
Одномерное дискретное случайное блуждание является цепью Маркова с целыми состояниями, чьё начальное распределение задаётся функцией вероятности случайной величины
 , а матрица переходных вероятностей имеет вид
, а матрица переходных вероятностей имеет вид ,
,
то есть
Теорема Донскера
Рассмотрим случайное блуждание
 , где
, где  .
.Центральная предельная теорема утверждает, что
 по распределению
по распределениюОднако, в случае случайных блужданий, это утверждение можно значительно усилить.
Построим по
 случайный процесс
случайный процесс ![S_n(t), t\in [0,1]](2ef7e7b14391904ef69d0531ac5eed49.png) , определив его следующим образом:
, определив его следующим образом:  , а при остальных
, а при остальных  мы доопределим процесс линейным продолжением:
мы доопределим процесс линейным продолжением:
Из центральной предельной теоремы

 по распределению
по распределениюЭто означает сходимость одномерных распределений процесса
 к одномерным распределениям винеровского процесса. Теорема Донскера, называемая также принципом инвариантности, утверждает, что имеет место слабая сходимость процессов,
к одномерным распределениям винеровского процесса. Теорема Донскера, называемая также принципом инвариантности, утверждает, что имеет место слабая сходимость процессов, 
Слабая сходимость процессов означает сходимость непрерывных по винеровской мере функционалов, то есть позволяет рассчитывать значения функционалов от броуновского движения (например максимума, минимума, последнего нуля, момента первого достижения уровня и других) предельным переходом от простого случайного блуждания.
См. также
Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей.Категории:- Случайные процессы
- Марковские процессы
- Технический анализ
Wikimedia Foundation. 2010.

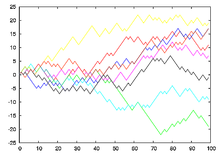
 восьми одномерных случайных блужданий.
восьми одномерных случайных блужданий.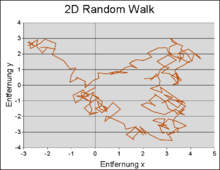
 до
до  , равновероятные направления
, равновероятные направления  или
или  .
.

