Одномерное стационарное уравнение Шрёдингера

Одномерное стационарное уравнение Шрёдингера — линейное обыкновенное дифференциальное уравнение второго порядка вида

$-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+U(x)\psi(x)=E\psi(x), \qquad ( 1 )$

где $\hbar$ — постоянная Планка, $\! m$ — масса частицы, $\! U(x)$ — потенциальная энергия, $\! E$ — полная энергия, $\! \psi(x)$ — волновая функция. Для полной постановки задачи о нахождении решения $\! ( 1 )$ надо задать также граничные условия, которые представляются в общем виде для интервала $\! [a,b]$

$\alpha_1\psi(a)+\beta_1\frac{d\psi(a)}{dx}=\gamma_1, \qquad ( 2 )$ $\alpha_2\psi(b)+\beta_2\frac{d\psi(b)}{dx}=\gamma_2, \qquad ( 3 )$

где $\! \alpha_1, \alpha_2, \beta_1, \beta_2, \gamma_1, \gamma_2$ — константы. Квантовая механика рассматривает решения уравнения $\! ( 1 )$, с граничными условиями $\! ( 2 )$ и $\! ( 3 )$.

Общие свойства

Исходя из физического смысла волновая функция должна быть однозначной и непрерывной функцией своих координат. Условие нормировки появляется из интерпретации квадрата волновой функции как вероятности.

$\int\limits_{-\infty}^{+\infty}|\psi(x)|^2dx=1. \qquad ( 0a )$

Отсюда следует, в частности, что волновая функция должна достаточно быстро спадать как функция x. В одномерном случае, если волновая функция $\! \psi(x)\sim1/x^\alpha$ при $\! x\longrightarrow +\infty$, то показатель степени в соответствии с выражением

$\! \int^{+\infty}|\psi(x)|^2dx=\int^{+\infty}1/x^{2\alpha}dx=1/x^{2\alpha-1}\mid^{+\infty} \longrightarrow 0, \qquad ( 0b )$

должен удовлетворять неравенству $\! \alpha>1/2.$

Интегрирование уравнения $\! ( 1 )$ в малой окрестности точки a даёт дополнительные условия на производную волновой функции

$\int^{a+\varepsilon}_{a-\varepsilon}\frac{d^2\psi(x)}{dx^2}dx= \frac{2m}{\hbar^2}\int^{a+\varepsilon}_{a-\varepsilon}(U(x)-E)\psi(x)dx, \qquad ( 0c )$

из которого в пределе $\! \varepsilon\longrightarrow 0$ следует

$\left.\frac{d\psi(x)}{dx}\right|_{a+0}-\left.\frac{d\psi(x)}{dx}\right|_{a-0} =0, \qquad ( 0d )$

если потенциальная энергия имеет в точке a разрывы первого рода (конечные скачки). Если же в точке a имеется разрыв второго рода, например потенциальная энергия описывается дельта-функцией ($\! U(x)=-G\delta(x-a)$), то условие $\! ( 0c )$ принимает вид

$\left.\frac{d\psi(x)}{dx}\right|_{a+0}-\left.\frac{d\psi(x)}{dx}\right|_{a-0} =\frac{2m}{\hbar^2}(-G)\psi(a). \qquad ( 0e )$

Если энергетический спектр невырожден, то существует только одна волновая функция, являющаяся решением уравнения Шрёдингера для данной энергии, причём она определена с точностью до фазы. В случае, когда потенциал симметричен, то волновые функции будут либо чётными, либо нечётными и чётность волновых функций чередуется.

Точные аналитические решения

В общем виде решения уравнения $\! ( 1 )$, с граничными условиями $\! ( 2 )$ и $\! ( 3 )$ не существует, но при некотором выборе потенциальной энергии можно найти точные решения. Они играют важную роль в построении аналитических приближенных решений уравнения $\! ( 1 )$.

Решение для свободной частицы — плоские волны

В свободном пространстве, где отсутствуют потенциалы уравнение $\! ( 1 )$ принимает особенно простой вид

$-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}=E\psi(x). \qquad ( 4 )$

Для этого уравнения решением является суперпозиция плоских волн

$\psi(x)=C_1 e^{i\sqrt{2mE}x/\hbar}+C_2 e^{-i\sqrt{2mE}x/\hbar}. \qquad ( 5 )$

Здесь энергия $\! E$ может принимать все значения выше нуля, поэтому говорят, что собственное значение принадлежит непрерывному спектру. Константы $\! C_1$ и $\! C_2$ определяются из условия нормировки.

Решение для частицы в одномерной потенциальной яме с бесконечно высокими стенками

Если поместить частицу в потенциальную яму, то непрерывный спектр энергий становится дискретным. Для уравнения $\! ( 1 )$ с потенциальной энергией $\! U(x)$, которая равна нулю в интервале $\! (0,a)$ и становится бесконечной в точках $\! 0$ и $\! a$. На этом интервале уравнение Шрёдингера совпадает с $\! ( 4 )$. Граничные условия $\! ( 2 )$, $\! ( 3 )$ для волновой функции запишутся в виде

$\! \psi(0)=0, \qquad ( 6 )$ $\! \psi(a)=0. \qquad ( 7 )$

Ищем решения в виде $\! A\sin{(\sqrt{2mE/\hbar^2}x+\delta)}$. С учётом граничных условий получаем для собственных значений энергии $\! E_n$

$\! E_n=\frac{\pi^2\hbar^2}{2ma^2}n^2 \qquad ( 8 )$

и собственных функций с учётом нормировки

$\! \psi_n(x)=\sqrt{\frac{2}{a}}\sin{\frac{\pi n}{a}x}. \qquad ( 9 )$

Численные решения

Сколько-нибудь сложный потенциал в уравнении $\! ( 1 )$ уже не позволяет найти аналитическое решение (вернее, это решение можно найти лишь для задачи об одной частице, движущейся в поле другой), и поэтому требуется привлекать численные методы для решения уравнения Шрёдингера. Одним из самых простых и доступных из них является метод конечных разностей, в котором уравнение $\! ( 1 )$ заменяется уравнением в конечных разностях на выбранной сетке с узлами в точках $\! x_n$, а именно, заменяя вторую производную по формуле

$\! \frac{d^2y(x)}{dx^2}=\frac{y_{n-1}-2y_n+y_{n+1}}{h^2}, \qquad ( 10 )$

где $\! h$ — шаг дискретизации, $\! n$ — номер узла сетки, получим

$\! -\frac{\hbar^2}{2m}\frac{y_{n-1}-2y_n+y_{n+1}}{h^2}+U_ny_n=Ey_n, \qquad ( 11 )$

где $\! U_n$ — значение потенциальной энергии $\! U(x)$ на узлах сетки. Пусть $\! a$ некоторый характерных масштаб потенциала, тогда уравнение $\! ( 11 )$ можно записать в безразмерном виде

$\! -y_{n-1}+(2+h^2\frac{2ma^2U_n}{\hbar^2})y_n-y_{n+1}=h^2\frac{2ma^2E}{\hbar^2}y_n. \qquad ( 12 )$

Если обозначить безразмерные величины потенциальной энергии $\! v_n=\frac{2ma^2U_n}{\hbar^2}$ и собственные значения $\! e=h^2\frac{2ma^2E}{\hbar^2}$, то уравнение $\! ( 12 )$ упростится

$\! -y_{n-1}+(2+v_n-e)y_n-y_{n+1}=0. \qquad ( 13 )$

Под последним выражением надо понимать систему уравнений для всех возможных индексов $\! n$.

Программный код^{[источник не указан 761 день]}

Используя уравнение в конечных разностях $\! ( 13 )$ запишем дискретный аналог для уравнения $\! ( 1 )$ с нулевым потенциалом

$\! -y_{n-1}+(2-e)y_n-y_{n+1}=0. \qquad ( 14 )$

Следующий программный код (Matlab) предназначен для решения уравнения $\! ( 14 )$ с нулевой потенциальной энергией и граничными условиями $\! ( 2 )$, $\! ( 3 )$.

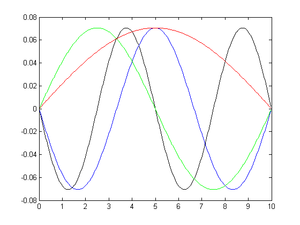
 clear;

%Размер матрицы
N=400;
%Число собственных значений
Roots=3;
%правая граница
a=10;
%Шаг дискретизации
step=a/(N+1);
%Сетка
s=step:step:a-step;
%% Потенциальная энергия
%% Вариант 1 - "большая яма"
  v=0*s;
%%Вариант 2 - 1/r потенциал
%v=1./linspace(-a,a,numel(s));
%v=-abs(v)*10; 
%%Вариант 3 - "вложенная потенциальная яма"
%v=abs(linspace(-a,a,numel(s)))<a/2;
%v=-abs(v)*10^3;
%% solution
figure('Name','Потенциал'); plot(v);ylim([-500 0]);
%Трёхдиагональная матрица
A=zeros(N);
for i=1:N
    A(i,i)=2+v(i)*step*step;
end
for i=1:N-1
    A(i,i+1)=-1;
    A(i+1,i)=-1;
end

%Вычисление собственных значений и собственных векторов
opts.isreal=0;
[psi,e]=eigs(A,Roots,'sr'); %верно считает состояния с отрицательной энергией
%[psi,e]=eigs(A,Roots,'sm');  %верно считает 'e'
for i=1:Roots
    e(i,i)=e(i,i)/(step*step);
end
%Вывод
e
%plot(s,psi(:,1),'k',s,psi(:,2),'b',s,psi(:,3),'g',s,psi(:,4),'r')
figure('Name','Fi');plot(s,psi);
legend_=(num2cell(1:size(psi,2)));
for i=1:numel(legend_)
    legend_{i} = num2str(legend_{i});
end
legend(legend_{:});

Собственные значения

 e =
 
     1.5790         0         0         0
          0    0.8882         0         0
          0         0    0.3948         0
          0         0         0    0.0987

На рисунке представлены четыре волновые функции, соответствующие собственным значениям $\! e$.

Первые четыре волновые функции — решения (1). Красная кривая — основное состояние, зелёная кривая — первое возбуждённое, синяя кривая и черная кривая соответствуют второму и третьему возбуждённым состояниям

Литература

• Боум А. Квантовая механика: основы и приложения. М. Мир, 1990. — 720с. ISBN 5-03-001311-3
• Березин Ф. А., Шубин М. А. Уравнение Шредингера. Изд-во МГУ, 1983.
• Калиткин. Н. Н. Численные методы. М., Наука, 1978.

Ссылки

• Particle in a box