- Теорема Лёвенгейма — Сколема
-
Теорема Лёвенгейма — Сколема
Теорема Лёвенгейма — Сколема — утверждение из теории моделей о том, что если множество предложений в счётном языке первого порядка имеет бесконечную модель, то оно имеет счётную модель. Эквивалентная формулировка: каждая модель счётной сигнатуры имеет счётную элементарную подмодель.
Эта теорема появилась в работе Лёвенгейма 1915-го года; она также часто называется теоремой Лёвенгейма — Сколема о понижении мощности (downward Löwenheim — Skolem theorem в англоязычной литературе), чтобы отличать её от похожего утверждения, называемого теоремой Лёвенгейма — Сколема о повышении мощности: если множество предложений счётного языка первого порядка имеет бесконечную модель, то оно имеет модель произвольной бесконечной мощности (upward Löwenheim — Skolem theorem).
Содержание
Набросок доказательства
Пусть структура
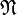 является моделью множества формул счётного языка
является моделью множества формул счётного языка 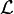 . Построим цепочку подструктур
. Построим цепочку подструктур 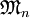 ,
, 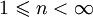 . Для каждой формулы
. Для каждой формулы 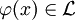 такой, что
такой, что 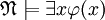 , обозначим через
, обозначим через  произвольный элемент модели, для которого
произвольный элемент модели, для которого 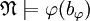 . Пусть
. Пусть 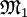 подструктура
подструктура 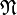 , сгенерированная множеством
, сгенерированная множеством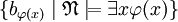
Индуктивно определим
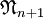 как подструктуру, сгенерированную множеством
как подструктуру, сгенерированную множеством
Так как количество формул счётно, каждая из подструктур
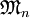 счётна. Заметим также, что их объединение удовлетворяет критерию Тарского — Вота, и следовательно является элементарной подструктурой
счётна. Заметим также, что их объединение удовлетворяет критерию Тарского — Вота, и следовательно является элементарной подструктурой 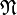 , что и завершает доказательство.
, что и завершает доказательство.Языки произвольной мощности
Теоремы Лёвенгейма — Сколема для языков произвольной мощности формулируются следующим образом:
Понижение мощности. Каждая структура сигнатуры мощности κ имеет элементарную подструктуру мощности мощности
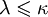 .
.Повышение мощности. Если множество предложений языка
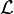 имеет бесконечную модель, то оно имеет модель любой мощности
имеет бесконечную модель, то оно имеет модель любой мощности  .
.Примеры
Связанные темы
- Теорема о компактности
- Критерий Тарского — Вота
- Элементарная эквивалентность
- Парадокс Сколема
Wikimedia Foundation. 2010.
Теорема Лёвенгейма-Сколема — … Википедия
Парадокс Сколема — представляет собой рассуждение, связанное с использованием теоремы Лёвенгейма Сколема для аксиоматической теории множеств. В отличие от парадокса Рассела, парадокса Кантора, парадокса Бурали Форти, где при помощи логически верных выводов… … Википедия
Теория моделей — Теория моделей раздел математической логики, который занимается изучением связи между формальными языками и их интерпретациями, или моделями. Название теория моделей было впервые предложено Тарским в 1954 году. Основное развитие теория … Википедия
Моделей теория — Теория моделей это раздел математической логики, который занимается изучением связи между формальными языками и их интерпретациями, или моделями. Название теория моделей было впервые предложено Тарским в 1954 году. Основное развитие теория… … Википедия
История математики — История науки … Википедия
Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия
Логика первого порядка — (исчисление предикатов) формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка. Содержание 1 … Википедия
