Примитивно рекурсивная функция

Термин рекурсивные функции в теории вычислимости используют для обозначения трёх множеств функций

• примитивно рекурсивные функции;
• общерекурсивные функции;
• частично рекурсивные функции.

Последние совпадают с множеством вычислимых по Тьюрингу функций. Определения этих трёх классов сильно связаны. Они были введены Куртом Гёделем с целью формализации понятия вычислимости.

Множество частично рекурсивных функции включает в себя множество общерекурсивных функции, а общерекурсивные функции включают в себя примитивно рекурсивные функции. Частично рекурсивные функции иногда называют просто рекурсивными функциями.

Примитивно рекурсивные функции

Определение

Определение понятия примитивно рекурсивной функции является индуктивным. Оно состоит из указания класса базовых примитивно рекурсивных функций и двух операторов (подстановки и примитивной рекурсии), позволяющих строить новые примитивно рекурсивные функции на основе уже имеющихся.

К числу базовых примитивно рекурсивных функций относятся функции следующих трёх видов:

• Нулевая функция O — функция без аргументов, всегда возвращающая 0.
• Функция следования S одного переменного, сопоставляющая любому натуральному числу x непосредственно следующее за ним натуральное число x + 1.
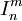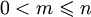• Функции $I_n^m$, где $0<m\leqslant n$, от n переменных, сопоставляющие любому упорядоченному набору 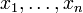$x_1,\dots, x_n$ натуральных чисел число x_m из этого набора.

Операторы подстановки и примитивной рекурсии определяются следующим образом:

• Оператор подстановки. Пусть f — функция от m переменных, а 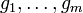$g_1, \dots, g_m$ — упорядоченный набор функций от n переменных каждая. Тогда результатом подстановки функций g_k в функцию f называется функция h от n переменных, сопоставляющая любому упорядоченному набору 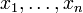$x_1, \dots, x_n$ натуральных чисел число

$h(x_1,\ldots,x_n)=f(g_1(x_1,\ldots,x_n),\ldots,g_m(x_1,\ldots,x_n))$.

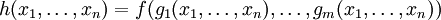• Оператор примитивной рекурсии. Пусть f — функция от n переменных, а g — функция от n + 2 переменных. Тогда результатом применения оператора примитивной рекурсии к паре функций f и g называется функция h от n + 1 переменной вида

$h(x_1,\ldots,x_n,0)=f(x_1,\ldots,x_n)$;

$h(x_1,\ldots,x_n,y+1)=g(x_1,\ldots,x_n,y,h(x_1,\ldots, x_n,y))$.

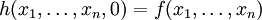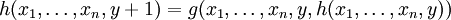Множество примитивно рекурсивных функций — это минимальное множество, содержащее все базовые функции и замкнутое относительно указанных операторов подстановки и примитивной рекурсии.

Примеры

Укажем на ряд широко известных арифметических функций, являющихся примитивно рекурсивных.

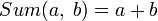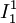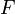• Функция Сложения двух натуральных чисел ($Sum(a,\;b)=a+b$) может быть рассмотрена в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения оператора примитивной рекурсии к функциям $I_1^1$ и $F\,\!$, вторая из которых получается подстановкой основной функции 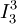$I_3^3$ в основную функцию S:

$Sum(x,\;0)=x$;

$Sum(x,\;y+1)=F(x,\;y,\;Sum(x,\;y))$;

$F(x,\;y,\;z)=S(I_3^3(x,\;y,\;z))$.

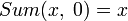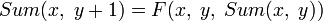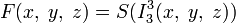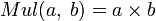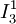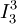• Умножение двух натуральных чисел ($Mul(a,\;b)=a\times b$) может быть рассмотрено в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения оператора примитивной рекурсии к функциям O и G, вторая из которых получается подстановкой основных функций $I_3^1$ и $I_3^3$ в функцию сложения:

$Mul(x,\;0)=O(x)$;

$Mul(x,\;y+1)=G(x,\;y,\;Mul(x,y))$;

$G(x,\;y,\;z)=Sum(I_3^1(x,\;y,\;z),I_3^3(x,\;y,\;z))$.

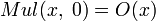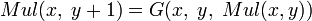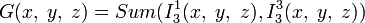• Симметрическая разность (абсолютная величина разности) двух натуральных чисел (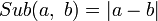$Sub(a,\;b)=|a-b|$) может быть рассмотрена в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения следующих подстановок и примитивных рекурсий:

$Sub(x,\;y)=Sum(Sub_1(x,\;y),\; Sub_2(x,\;y))$;

$Sub_2(x,\;y)=Sub_1(I_2^2(x,\;y),\; I_2^1(x,\;y))$;

$\left\{\begin{array}{l}Sub_1(x,\;0)=I_1^1(x)\\ Sub_1(x,\;y+1)=f(x,\;y,\;Sub_1(x,\;y))\end{array}\right.$;

$f(x,\;y,\;z)=p(I_3^3(x,\;y,\;z))$;

$\left\{\begin{array}{l}p(0)=0\\ p(y+1)=I_2^1(y,\;p(y))\end{array}\right.$;

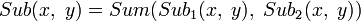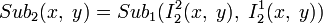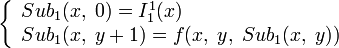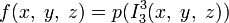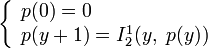Частично рекурсивные функции

Частично рекурсивные функции определяются аналогичным образом, только к двум операторам подстановки и примитивной рекурсии добавляется ещё оператор минимизации аргумента.

• Оператор минимизации аргумента. Пусть f — функция от n  натуральных переменных. Тогда результатом применения оператора минимума аргумента к функции f называется функция h от n − 1 переменной, задаваемая следующим определением:

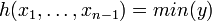$h(x_1,\ldots, x_{n-1}) = min (y)$, при условии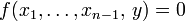 $f(x_1,\ldots,x_{n-1},\,y)=0$

То есть функция h возвращает минимальное значение последнего аргумента функции f, при котором её значение равно 0.

Интересно отметить аналогию с императивными языками программирования. Примитивные функции соответствуют программным функциям, в которых используется только арифметические операции, а также условный оператор и оператор арифметического цикла (оператор цикла, в котором число итераций известно на момент начала цикла).

Если же программист начинает использовать оператор цикла while, в котором число итераций заранее неизвестно, и в принципе, может быть бесконечным, то он переходит в класс частично рекурсивных функций.

Важным моментом является то, что частично рекурсивные функции для некоторых значений аргумента могут быть не определены, так как оператор минимизации аргумента не всегда корректно определён, именно, функция f может быть не равной нулю ни при каких значениях аргументов.

Собственно, оттого, что частично рекурсивные функции могут иметь корректно определённое значение лишь на части аргументов, и пошло их название.

С точки зрения программиста результатом частично рекурсивной функции может быть не только число, но и исключение (Exception) или «зависание», соответствующее неопределённому значению.

Общерекурсивные функции

Общерекурсивные функции — это подмножество частично рекурсивных функций, определённых для всех значений аргументов. Задача определения того, является ли частично рекурсивная функция с данным описанием общерекурсивной или нет, алгоритмически неразрешима.

Свойства

Легко понять, что любая примитивно рекурсивная функция является частично рекурсивной, так как по определению операторы для построения частично рекурсивных функций включают в себя операторы для построения примитивно рекурсивных функций.

Также понятно, что примитивно рекурсивная функция определена везде и поэтому является общерекурсивной функцией (у примитивно рекурсивной функции нет повода «зависать», так как при её построении используются операторы, определяющие везде определённые функции).

Довольно сложно доказать существование и привести пример общерекурсивной функции, не являющейся примитивно рекурсивной. Одним из популярных примеров является функция Аккермана.

Как было показано Гёделем, частично рекурсивные функции совпадают с множеством вычислимых функций.

История возникновения названий

Термины «частично рекурсивная функция» и «общерекурсивная функция» прижились в силу исторических причин и по сути являются результатом неточного перевода английских терминов partial recursive function и total recursive function, которые по смыслу более правильно переводить как «рекурсивные функции, определенные на части множества возможных аргументов» и «рекурсивные функции, определенные на всём множестве возможных аргументов». Наречие «частично» относится не к прилагательному «рекурсивные», а к области определения функции. Возможно, более правильным названием было бы «частично определённые рекурсивные функции» и просто «везде определённые рекурсивные функции». Но длинные названия не прижились.

См. также

Другие абстрактные исполнители и формальные системы вычислений

• Алгоритм Маркова (продукционное программирование)
• Машина Тьюринга (автоматное программирование)
• Машина Поста (автоматное программирование)
• Лямбда-исчисление (функциональное программирование)
• императивное программирование)

Литература

• Гильберт Д, Бернайс П. Основания математики, Т. 1. — М.: Наука, 1979.
• Клини С. К. Введение в метаматематику. — М., 1957.
• Петер Р. Рекурсивные функции — ИЛ, 1954.
• Верещагин Н. К., Шень А.Лекции по математической логике и теории алгоритмов. Часть 3. Вычислимые функции, 2-е изд., исправленное. — М.:МЦНМО, 2002.