Модель Лотки — Вольтерра

Модель Лотки — Вольтерра

Модель Лотки — Вольтерра — модель межвидовой конкуренции, названная в честь её авторов — (Лотка, 1925; Вольтерра 1926), которые предложили модельные уравнения независимо друг от друга.

Такие уравнения можно использовать для моделирования систем «хищник-жертва», «паразит-хозяин», конкуренции и других видов взаимодействия между двумя видами (Одум, 1986)

В математической форме предложенная система имеет следующий вид:

$\ \frac{{\rm d}x}{{\rm d}t}=(\alpha -\beta y)x$

$\ \frac{{\rm d}y}{{\rm d}t}=(-\gamma +\delta x) y,$

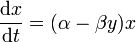
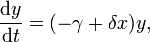
где:

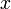• $\ x$ — количество жертв
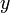• $\ y$— количество хищников
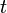• $\ t$ — время
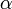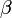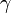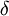• $\ \alpha$, $\ \beta$, $\ \gamma$ и $\ \delta$ — коэффициенты, отражающие взаимодействия между видами

Решение системы уравнений

Постановка задачи

Допустим у нас есть закрытый ареал из которого существа ни иммигрируют, ни эммигрирует. Также допустим, что еды для травоядных животных у нас имеется с избытком. Тогда уравнение изменения количества жертв примет вид:

$~\frac{dx}{dt}=\alpha x,$

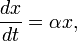
где:

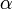• $~\alpha$ — это коэффициент рождаемости жертв
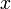• $~x$ — это величина популяции жертв
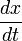• $~\frac{dx}{dt}$ — это скорость прироста популяции жертв.

Так как хищники стабильным питанием не обеспечены, то они вымирают. Следовательно уравнение для хищников примет вид:

$\frac{dy}{dt}=-\gamma y,$

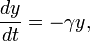
где:

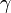• $~\gamma$ — это коэффициент убыли хищников
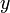• $~y$ — это величина популяции хищников
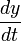• $~\frac{dy}{dt}$ — это скорость прироста популяции хищников.

Встречи хищников и жертв(которые 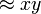$~\approx xy$), убивают жертв с коэффициентом 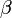$~\beta$ и рождают новых хищников с коэффициентом 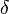$~\delta$. С учётом этого, получаем систему уравнений: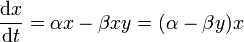

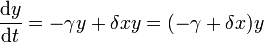
$\ \frac{{\rm d}x}{{\rm d}t}=\alpha x -\beta x y = (\alpha -\beta y)x$

$\ \frac{{\rm d}y}{{\rm d}t}=-\gamma y +\delta x y = (-\gamma +\delta x) y$

Решение задачи

Нахождение стационарной позиции системы

Найдем стационарную точку, вокруг которой происходят колебания. Для стационарной позиции изменение популяции равно нулю. Следовательно:

$~\alpha \bar{x} -\beta \bar{x} \bar{y} = 0$

$~-\gamma \bar{y} +\delta \bar{x} \bar{y} = 0$

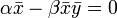
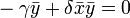
Из чего следует, что:

$\bar{x}=\frac{\gamma}{\delta}$

$\bar{y}=\frac{\alpha}{\beta}$

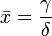
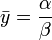
Задание отклонения системе

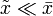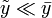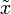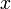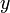Теперь на надо ввести в нашу систему колебания $~\tilde{x} \ll \bar{x}$ и $~\tilde{y} \ll \bar{y}$. Из-за малой величины квадратами, кубами и т.д. $\tilde{x}$ можно пренебречь. Теперь популяция $~x$ и $~y$ будет равняться: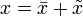

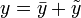
$~x=\bar{x}+\tilde{x}$

$~y=\bar{y}+\tilde{y}$

Далее расписываем предыдущее уравнение:

$\frac{d\tilde{x}}{dt}=\alpha (\bar{x}+\tilde{x}) -\beta (\bar{x}+\tilde{x}) (\bar{y}+\tilde{y})=\frac{\alpha\gamma}{\delta}+\alpha\tilde{x}-\frac{\beta\gamma\alpha}{\delta\beta}-\frac{\beta\gamma}{\delta}\tilde{y}-\frac{\beta\alpha}{\beta}\tilde{x}-\beta\tilde{x} \tilde{y}=-\frac{\beta\gamma}{\delta} \tilde{y}$

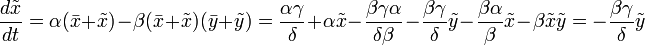
Похожий ответ получаем относительно хищников:

$\frac{d\tilde{y}}{dt}=\frac{\delta \alpha}{\beta} \tilde{x}$

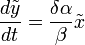
После чего дифференцируем одно уравнение и подставляем в него другое:

$\frac{d^2\tilde{x}}{dt}=-\frac{\beta\gamma}{\delta}\frac{\delta\alpha}{\beta}\tilde{x}=-\alpha\gamma\tilde{x}$

$\frac{d^2\tilde{x}}{dt}+\alpha\gamma\tilde{x}=0$

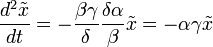
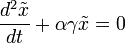
— является уравнением гармонического осциллятора с периодом $T=\frac{2\pi}{\sqrt{\alpha\gamma}}$

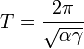
См. также

Система «хищник-жертва»

Ссылки

• Популяционная динамика
• Простейшая модель «хищник-жертва»