N-мерный тетраэдр

N-мерный тетраэдр

N-мерный тетраэдр — простейший возможный в N-мерном пространстве многогранник. Является обобщением для N-мерного пространства таких фигур, как треугольник и трёхмерный тетраэдр.

Построение

Преобразование 1-тетраэдра в 2-тетраэдр

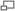
Преобразование 2-тетраэдра в 3-тетраэдр

Как известно, через любые N точек можно провести (N–1)–плоскость и существуют множества из N+1 точек, через которые (N–1)–плоскость провести нельзя. Таким образом, N+1 – минимальное число точек в N–пространстве, которое не лежит в одной (N–1)–плоскости, и может служить вершинами N–многогранника.

Простейший N–многогранник с количеством вершин N+1 называется N–тетраэдром по названию трёхмерного члена этого семейства. В литературе принято также название «симплекс». В пространствах низшей размерности этому определению соответствуют 4 фигуры:

• 0-тетраэдр (точка) – 1 вершина;
• 1–тетраэдр (отрезок) – 2 вершины;
• 2–тетраэдр (треугольник) – 3 вершины;
• 3–тетраэдр (собственно тетраэдр) – 4 вершины.

Все эти фигуры обладают тремя общими свойствами:

1. В соответствии с определением, число вершин у каждой фигуры на единицу больше размерности пространства;

2. Существует общее правило преобразования фигур низшей размерности в фигуры высшей размерности. Оно заключается в том, что из геометрического центра фигуры строится перпендикуляр в следующее измерение, на этом перпендикуляре строится новая вершина и соединяется рёбрами со всеми вершинами исходного тетраэдра;

3. Как следует из описанной в п. 2 процедуры, любая вершина тетраэдра соединена рёбрами со всеми остальными вершинами.

Описанная сфера

Построение описанной 2-сферы вокруг 1-тетраэдра с дополнительной точкой

Вокруг любого N-тетраэдра можно описать N-сферу.

Для 1-тетраэдра это утверждение очевидно. Описанная 1-сфера будет представлять собой отрезок, совпадающий с самим 1-тетраэдром, и её радиус будет составлять R = a/2. Добавим к 1-тетраэдру ещё одну точку и попробуем описать вокруг них 2-сферу.

Построим 2-сферу s₀ радиусом a/2 таким образом, чтобы отрезок AB был её диаметром. Если точка С находится за пределами окружности s₀, то увеличивая радиус окружности и смещая её в сторону точки С можно добиться того, что все три точки окажутся на окружности. Если же точка С лежит внутри окружности s₀, то подогнать окружность под эту точку можно увеличивая её радиус и смещая в сторону, противоположную точке С. Как видно из рисунка, сделать это можно в любом случае, когда точка С не лежит на одной прямой с точками АВ. Не является помехой и несимметричное расположение точки С относительно АВ.

Рассматривая общий случай, предположим, что существует (N–1)-сфера S_N-1 радиуса r, описанная вокруг некоторой (N–1)-мерной фигуры. Поместим центр сферы в начало координат. Уравнение сферы будет иметь вид

$x_1^2+x_2^2+x_3^2+ ... + x_{N-1}^2 = r^2. \qquad (1)$

Построим N-сферу с центром в точке (0, 0, 0, ... 0, h_S) и радиусом R, причём

$R^2=r^2+h_S^2.$

Уравнение этой сферы

$x_1^2+x_2^2+x_3^2+ ... + x_{N-1}^2+{x_N-h_S}^2 = r^2+h_S^2$

или

$x_1^2+x_2^2+x_3^2+ ... + x_{N-1}^2 = r^2-x_N^2+2x_Nh_S. \qquad (2)$

Подставив в уравнение (1) x_N = 0, получим уравнение (2). Таким образом, при любом h_S сфера S_N-1 является подмножеством сферы S_N, а именно – её сечением плоскостью x_N = 0.

Предположим, что точка С имеет координаты (X₁, X₂, X₃, ..., X_N ). Преобразуем уравнение (2) к виду

$x_1^2+x_2^2+x_3^2+ ... + x_{N-1}^2 + x_N^2 = r^2+2x_Nh_S$

и подставим в него координаты точки С:

$X_1^2+X_2^2+X_3^2+ ... + X_{N-1}^2 + X_N^2 = r^2+2X_Nh_S.$

Выражение в левой части представляет собой квадрат расстояния R_C от начала координат до точки C, что позволяет привести последнее уравнение к виду

$R_C^2 = r^2+2X_Nh_S,$

откуда можно выразить параметр h_S:

$h_S = \frac{R_C^2-r^2}{2X_N}.$

Очевидно, что h_S существует при любых R_C, X_N и r, кроме X_N = 0. Это значит, что если точка С не лежит в плоскости сферы S_N–1, всегда можно найти такой параметр h_S, что на сфере S_N c центром (0, 0, 0, ..., h_S) будет лежать и сфера S_N–1, и точка С. Таким образом, вокруг любых N+1 точек можно описать N–сферу, если N из этих точек лежат на одной (N–1)–сфере, и последняя точка не лежит с ними в одной (N–1)–плоскости.

Применяя последнее по индукции, можно утверждать, что N–сферу можно описать вокруг любых N+1 точек, если они не лежат в одной (N–1)–плоскости.

Число граней N-тетраэдра

Тетраэдр имеет N+1 вершин, каждая из которых соединена рёбрами со всеми остальными вершинами.

Поскольку все вершины тетраэдра соединены между собой, то тем же свойством обладает и любое подмножество его вершин. Это значит, что любое подмножество из L+1 вершин тетраэдра определяют его L–мерную грань, и эта грань сама является L–тетраэдром. Тогда для тетраэдра число L-мерных граней равно числу способов выбрать L+1 вершину из полного набора N+1 вершин.

Обозначим символом К(L,N) число L–мерных граней в N–многограннике, тогда для N-тетраэдра

$~K(L,N) = C^{L+1}_{N+1},$

где $~C^m_n$ – число сочетаний из n по m.

В частности, число граней старшей размерности равно числу вершин и равно N+1:

$~K(0,N) = K(N-1,N) = N+1.$

Формулы для правильного N-тетраэдра

Число L-мерных граней	$~K(L,N) = C^{L+1}_{N+1}$
Высота	$~H_N = a\sqrt{\frac{N+1}{2N}}$	$~H_N = R_N \frac{N+1}{N}$	$~H_2 = a \frac{\sqrt{3}}{2}$	$~H_3 = a \frac{\sqrt{6}}{3}$	$~H_4 = a \frac{\sqrt{10}}{4}$
Объём	$~V_N = \frac{a^N}{N!}\sqrt{\frac{N+1}{2^N}}$	$~V_N = \frac{R^N_N}{N!} \sqrt{\left( \frac{N+1}{N} \right)^N}$	$~V_2 = a^2 \frac{\sqrt{3}}{4}$	$~V_3 = a^3 \frac{\sqrt{2}}{12}$	$~V_4 = a^4 \frac{\sqrt{5}}{96}$
Радиус описанной сферы	$~R_N = a\sqrt{\frac{N}{2(N+1)}}$	$~a = R_N \sqrt{\frac{2(N+1)}{N}}$	$~R_2 = a \frac{\sqrt{3}}{3}$	$~R_3 = a \frac{\sqrt{6}}{4}$	$~R_4 = a \frac{\sqrt{10}}{5}$
Радиус вписанной сферы	$~r_N = \frac{a}{\sqrt{2N(N+1)}}$	$~r_N = \frac{R_N}{N}$	$~r_2 = a \frac{\sqrt{3}}{6}$	$~r_3 = a \frac{\sqrt{6}}{12}$	$~r_4 = a \frac{\sqrt{10}}{20}$
Двугранный угол	$~\cos \alpha = \frac{1}{N}$

Несколько полезных соотношений

$~R_N = H_N \frac{N}{N-1}$

$~a^2 = H_N^2 + R_{N-1}^2$

$~V_N = \frac{1}{N}V_{N-1}H_N$

$~r_N = R_N^2 - R_{N-1}^2$